R语言教程
数据:是指对客观事件进行记录并可以鉴别的符号,是对客观事物的性质、状态以及相互关系等进行记载的物理符号或这些物理符号的组合。
R语言的特点:
1、有效的数据处理和保存机制:
R语言官网:httpsmmmmmmmmmfadsfa://www.r-project.org/
推荐书籍:《R语言实战》
常用快捷键:Ctrl + L 清空终端
R语言基础
1.1 R语言的基本功能
在Linux系统中,R语言中可以通过以下命令启动R软件
可以通过以下命令来查找每个命令如何使用:
通过以下命令可以获取当前目录:
可以通过Rprofile.site对R软件进行全局设置,Rprofile.site文件地址为D:\R\R-4.2.1\etc,这个文件中通过 # 进行注释,可以在最后通过.First()或者.Last(),当开始运行R软件时会执行.First()中的内容,当关闭R软件时执行.Last()中的内容。
.First()中可以是常用的库,也可以是自己编写的常用函数的源代码文件。
.Last()中可以是保存程序输出或者保存数据文件等。
在Rstudio软件中在命令后加括号进行区分对象和函数,R语法中对象可以是常量、变量,也可以是函数等等,函数必须加括号,便于区分。
可以通过setwd命令设定工作空间(这里是斜线,不是windows的反斜线):
1 > setwd( dir = "f:/Code/Code_R/R_proj_01" )
可以通过list.files()命令查看当前目录下的文件:
R中不需要进行变量申明,可以进行变量赋值和计算,但是变量名不能以数字开头。
在终端中有以下三种赋值方式:
1 2 3 > x <- 3> 6 -> y> z = 10
通过xx <<- 9命令对全局变量进行强制赋值:
在终端中通过ls()可以列出当前工作空间的变量:
ls()命令是无法看到隐藏文件(以.开头的文件)的。可以通过以下命令查看所有文件(包括隐藏文件):
在终端中通过list.files()命令列出当前文件夹下的文件:
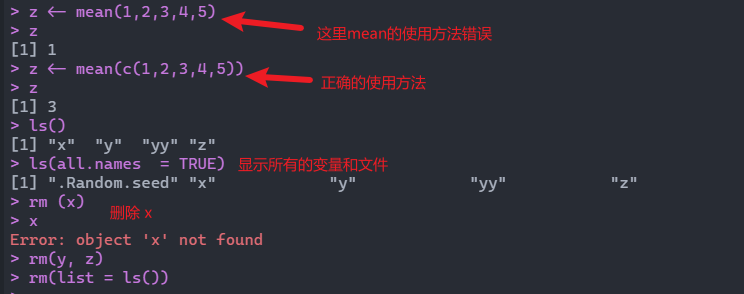
删除变量通过rm命令,如下所示,分别为删除单个变量、多个变量和所有变量:
1 2 3 > rm( x) > rm( y, z) > rm( list = ls( ) )
通过Ctrl + L将终端所有代码清屏。
为了避免电脑死机,通过save.image()保存工作空间:
在终端中输入q()退出软件:
相应的操作结果图如下:
R表达式中常用的符号:
1.2 R包的安装
R包的安装:
推荐使用在线安装的方式,可以自动安装需要的依赖包。
R中使用字符串要加引号,不加引号会将字符串当作对象处理,程序找不到对象就会报错:
错误用法:
正确用法:
1 2 3 > install.packages( "vcd" ) > install.packages( c ( "tidyr" , "dplyr" ) )
可以通过以下命令查看库所在的位置:
也可以通过以下命令查看库中所有的包:
如果想一次安装多个包,可以通过以下命令:
1 > install.packages( c ( "AER" , "ca" ) )
使用update.packages()命令可以更新安装的软件包:
1.3 R包的使用
下载安装完包后,载入包就不需要引号了,如下:
正确用法:
或者通过require加载包:
R软件自带的包有:base,datasets,utils,grDevices,graphics,stats,methods,splines,stats4,tcltk
base:R基础功能相关的函数
datasets:存放R内置的数据集
grDevices:基于grid绘图相关的设备
graphics:基于base图形的R函数,R的绘图函数都在这个包中
methods:R语言一般的定义方法和类
这些包提供了种类繁多的函数和数据集,这些包集合在一起构成了R软件。
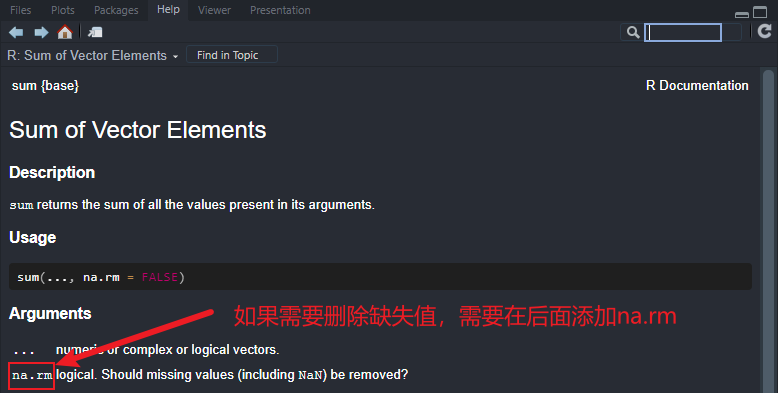
通过帮助文档进行R包的学习和使用:
也可以通过以下命令查看包的基础信息:
可以通过ls("package:函数包名")查看包的所有函数,例如:
可以通过data("package:函数包名")查看包的所有数据集,例如:
可以通过detach("package:函数包名")移除加载的包,例如:
可以通过remove.packages函数彻底删除包:
1 > remove.packages( "vcd" )
将R包迁移到新设备,通过以下步骤进行操作 :
列出当前环境已安装的包
取第1列,即所有包的名字,并保存给变量Rpack
1 > Rpack <- installed.packages( ) [ , 1 ]
将所有的包保存到Rpack.Rdata文件中
1 > save( Rpack, file= "Rpack.Rdata" )
将Rpack.Rdata文件移入新设备,在新设备上R软件终端中通过以下命令安装R包:
1 > for ( i in Rpack) install.packages( i)
即使新设备已经安装了包,R会自动跳过已经安装的包。
1.4 获取帮助
R软件的帮助文档可以通过help命令进行查看:
或者通过菜单栏中的help进行查看。
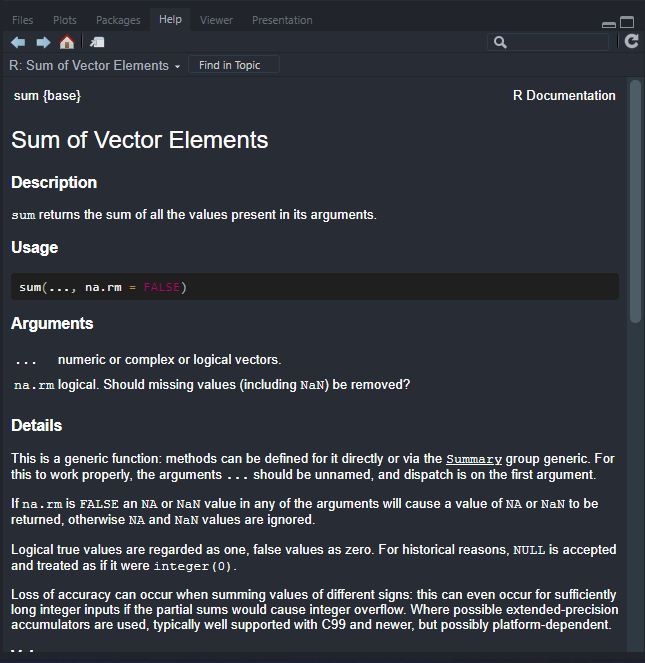
示例:在终端中
或者?也可以:
运行结果:
如果想直接了解函数中的参数,可以通过args函数:
在帮助文档中可以根据example中示例进行学习,也可以在终端中输入example进行实例展示:
也可以通过以下命令展示绘图demo:
如果想查看某个包的帮助文档,可以通过如下命令:
有些R包包含vignette文档,这个文档包含简介,教程文档等,但也并不是所有的包都有:
有时候明明已经安装了包,但是help搜索不到相应的函数,这是因为相关的包并没有加载,需要通过library进行加载,如果不加载,可以通过以下方式搜索:
通过包的名字:help(package = vcd)
需要通过双问号命令进行搜索,例如:
有些情况下不知道函数名,可以通过help.search进行本地模糊搜索:
1 > help.search( "heatmap" )
这里的help.search可以通过??来简写:
apropos函数可以列出所有包含关键字的内容,例如:
apropos函数也可以限定搜索范围,比如仅仅对函数进行搜索:
1 > apropos( "sum" , mod= "function" )
也可以通过RSiteSearch进行官网搜索:
==注意==:help.search为本地搜索
也可以通过 https://rseek.org/ 进行搜索,前提是要能够使用Google搜索。
1.5 内置数据集
R软件内置数据集存放在datasets中,某人加载这个包。
可以通过help查看数据集的具体内容:
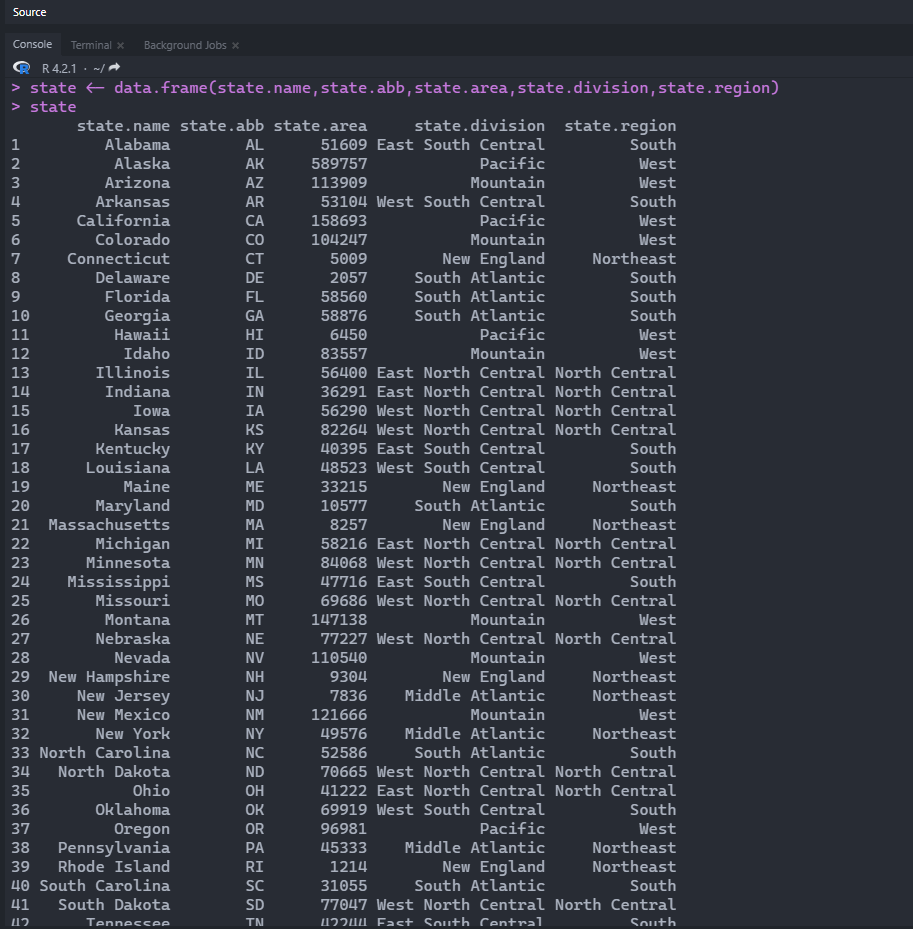
可以将一些数据组成数据框,示例:
1 2 > state <- data.frame( state.name, state.abb, state.area, state.division, state.region) > state
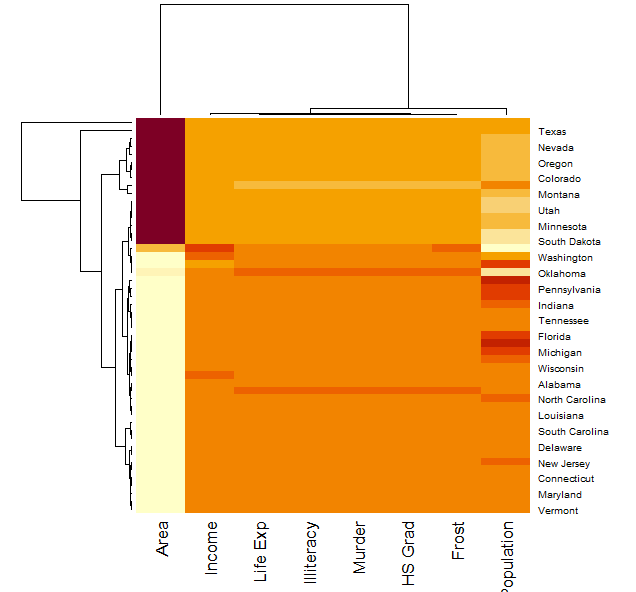
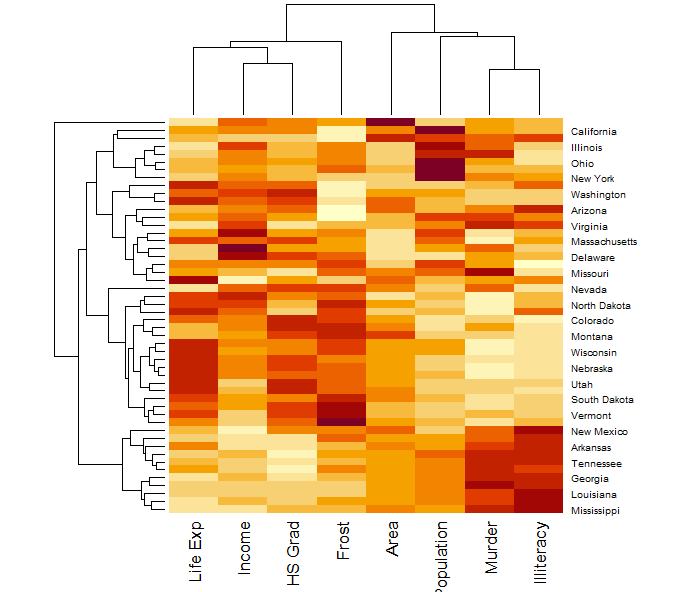
有些数据集可以绘制对应的热图:
可以通过如下操作查看某个包中的数据集:
可以通过如下操作查看R软件中所有数据集(包括自己安装的包的数据集):
1 > data( package= .packages( all.available = TRUE ) )
如果不想加载某个数据集,但是想用其数据集,可以通过以下命令(Chile为数据集,car为包名):
1 > data( Chile, package= "car" )
2 数据结构
R语言中最重要的概念是对象。
对象:object,它是指可以赋值给变量的任何事物,包括常量、数据结构、函数,甚至图形。对象都拥有某个模式,描述了此对象是如何存储的,以及某个类。
2.1 向量
向量,vector,是R中最重要的一个概念,它是构成其他数据结构的基础。R中的向量概念与数学中向量是不同的,类似于数学上的集合的概念,由一个或多个元素构成。
向量其实是用于存储数值型、字符型或逻辑型数据结构的一维数组。
用函数c来创建向量。c代表concatenate连接,也可以理解为收集collect,或者合并combine,例如:
这里的x就是向量,也可以称为对象。
在R语言中字符串要加引号,如果不加引号,就会把字符串当成对象。
1 > y <- c ( "one" , "two" , "three" )
对于逻辑型变量用TRUE、FALSE、T、F进行表示:
1 > z <- c ( TRUE FALSE TRUE FALSE )
不能够用首字母大写的模式,如 True 或 False。
用冒号构建等差数列:
如果想调整等差数列的差值,可以通过seq函数:
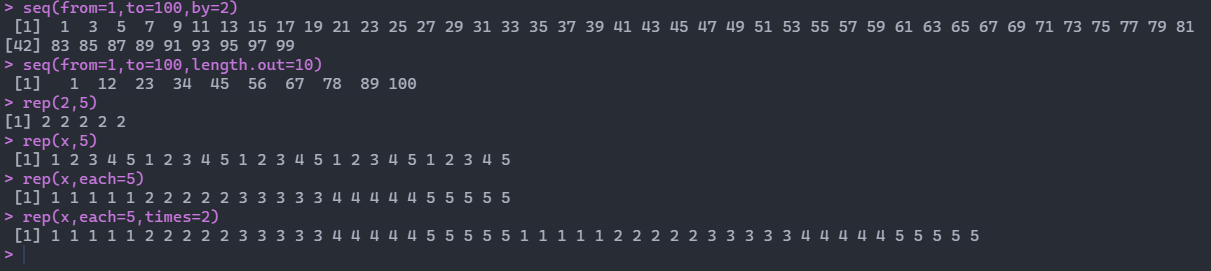
1 > seq( from= 1 , to= 100 , by= 2 )
如果想等差生成10个值,可以通过如下方式:
1 > seq( from= 1 , to= 100 , length.out= 10 )
如果想要输出重复的数值,可以通过rep函数,比如重复5次2:
还有其他用法:x = 1 2 3 4 5
将x向量依次重复5次:
输出:1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
将x向量每个元素重复5次:
输出:1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5
将x向量每个元素依次重复五次,并执行两次:
输出:1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5
示例:
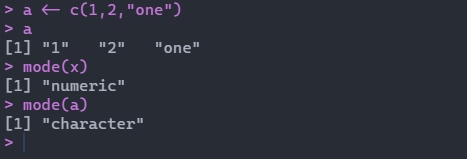
向量的数据类型都是同一类型,都是数值型或者字符型。如果不是同一类型,会自动将其转换为同一类型:
通过如果想要查看变量的类型,可以通过mode函数进行查看。
如果想要提取出x中大于3的值:
输出:4 5
例如前面的重复,也可以进行批量处理:
输出:1 1 2 2 2 2 3 3 3 3 3 3 4 5 5 5
2.2 向量索引
可以用length统计向量的长度,R中元素序列是从0开始。
x[-19]表示不显示第19个数值。
x[c(1,23,45,67,89)]表示输出对应位置的数值
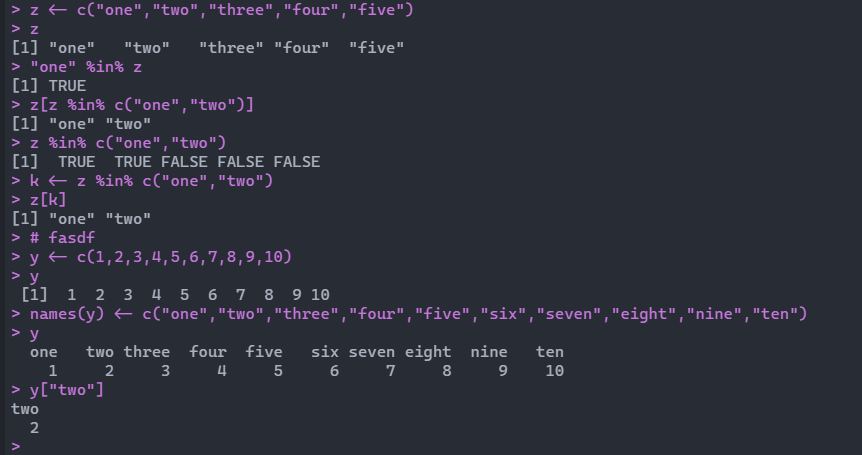
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 > y <- c ( 1 : 10 ) [ 1 ] 1 2 3 4 5 6 7 8 9 10 > y[ c ( T , F , T , F , T , F , T , F , T , F ) ] [ 1 ] 1 3 5 7 9 > y[ c ( T , F , T , F , T , F , T , F , T , F ) ] [ 1 ] 1 3 5 7 9 > y[ c ( T , F ) ] [ 1 ] 1 3 5 7 9 > y[ c ( T , F , F ) ] [ 1 ] 1 4 7 10 > y[ y> 5 ] [ 1 ] 6 7 8 9 10 > y[ y> 5 & y< 9 ] [ 1 ] 6 7 8 > z <- c ( "one" , "two" , "three" , "four" , "five" ) > z [ 1 ] "one" "two" "three" "four" "five" > "one" %in% z [ 1 ] TRUE > z[ z %in% c ( "one" , "two" ) ] [ 1 ] "one" "two" > z %in% c ( "one" , "two" ) [ 1 ] TRUE TRUE FALSE FALSE FALSE > k <- z %in% c ( "one" , "two" ) > z[ k] [ 1 ] "one" "two"
也可以通过names函数对变量进行命名:
1 2 3 4 5 6 7 8 9 10 > y <- c ( 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ) > y [ 1 ] 1 2 3 4 5 6 7 8 9 10 > names ( y) <- c ( "one" , "two" , "three" , "four" , "five" , "six" , "seven" , "eight" , "nine" , "ten" ) > y [ 1 ] one two three four five six seven eight nine ten [ 2 ] 1 2 3 4 5 6 7 8 9 10 > y[ "two" ] [ 1 ] two [ 2 ] 2
添加和删除元素:x为1到100的向量
1 2 3 4 5 6 > x[ 101 ] <- 101 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [ 31 ] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 [ 61 ] 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 [ 91 ] 91 92 93 94 95 96 97 98 99 100 101
还可以通过以下方式添加向量:
1 2 3 4 5 6 7 8 9 10 11 12 13 > v <- 1: 3 > v [ 1 ] 1 2 3 > v[ c ( 4 , 5 , 6 ) ] <- c ( 4 , 5 , 6 ) > v [ 1 ] 1 2 3 4 5 6 > v[ 20 ] <- 4 > v [ 1 ] 1 2 3 4 5 6 NA NA NA NA NA NA NA NA NA NA NA NA NA 4 > append( x = v, values = 99 , after = 5 ) [ 1 ] 1 2 3 4 5 99 6 NA NA NA NA NA NA NA NA NA NA NA NA NA 4 > append( x = v, values = 88 , after = 0 ) [ 1 ] 88 1 2 3 4 5 6 NA NA NA NA NA NA NA NA NA NA NA NA NA 4
如果想要删除某个元素:
方法一:
方法二:通过不显示想删除的部分,然后赋值给自身就相当于删除部分元素了
如果想替换某个元素:
不能够将字符串赋值给数值,否则都会变成字符串。
2.3 向量运算
向量的基本用法:
1 2 3 4 5 6 7 8 9 10 > x <- 1: 10 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 > x+ 1 [ 1 ] 2 3 4 5 6 7 8 9 10 11 > x- 3 [ 1 ] - 2 - 1 0 1 2 3 4 5 6 7 > x <- x+ 1 > x [ 1 ] 2 3 4 5 6 7 8 9 10 11
总结:+为给所有元素相加某一值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > x [ 1 ] 2 3 4 5 6 7 8 9 10 11 > y <- seq( 1 , 100 , length.out = 10 ) > y [ 1 ] 1 12 23 34 45 56 67 78 89 100 > x* y [ 1 ] 2 36 92 170 270 392 536 702 890 1100 > x** 2 [ 1 ] 4 9 16 25 36 49 64 81 100 121 > x^ 2 [ 1 ] 4 9 16 25 36 49 64 81 100 121 > x%% y [ 1 ] 0 3 4 5 6 7 8 9 10 11 > x%/% 5 [ 1 ] 0 0 0 1 1 1 1 1 2 2
总结:*为元素相乘符,**和^均为幂运算,%%为取余符号,%/%为整除符号。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 > z <- c ( 1 , 2 ) > z[ 1 ] 1 2 > x [ 1 ] 2 3 4 5 6 7 8 9 10 11 > x+ z [ 1 ] 3 5 5 7 7 9 9 11 11 13 > x = c ( 1 , 2 , 3 ) > x[ 1 ] 1 2 3 > x+ z[ 1 ] 2 4 4 Warning message: In x + z : longer object length is not a multiple of shorter object length
总结:长的向量和短的向量相加,长的向量中元素个数必须为短的向量个数的整数倍。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 > x <- 1: 10 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 > y <- seq( 1 , 100 , length.out = 10 ) > y [ 1 ] 1 12 23 34 45 56 67 78 89 100 > x> 5 [ 1 ] FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE > x> y [ 1 ] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE > c ( 1 , 2 , 3 ) %in% c ( 1 , 2 , 2 , 4 , 5 , 6 ) [ 1 ] TRUE TRUE FALSE > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 > y [ 1 ] 1 12 23 34 45 56 67 78 89 100 > x== y [ 1 ] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE > x <- - 5 : 5 > x [ 1 ] - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 > abs ( x) [ 1 ] 5 4 3 2 1 0 1 2 3 4 5 > sqrt ( 25 ) [ 1 ] 5 > log ( 16 , base = 2 ) [ 1 ] 4 > log ( 16 ) [ 1 ] 2.772589 > log ( 16 , base = 10 ) [ 1 ] 1.20412 > log10( 10 ) [ 1 ] 1 > x [ 1 ] - 5 - 4 - 3 - 2 - 1 0 1 2 3 4 5 > exp ( x) [ 1 ] 6.737947e-03 1.831564e-02 4.978707e-02 1.353353e-01 3.678794e-01 1.000000e+00 2.718282e+00 7.389056e+00 2.008554e+01 [ 10 ] 5.459815e+01 1.484132e+02 > ceiling ( c ( - 2.3 , 3.1415 ) ) [ 1 ] - 2 4 > floor ( c ( - 2.3 , 3.1415 ) ) [ 1 ] - 3 3 > trunc ( c ( - 2.3 , 3.1415 ) ) [ 1 ] - 2 3 > round ( c ( - 2.3 , 3.1415 ) ) [ 1 ] - 2 3 > round ( c ( - 2.3 , 3.1415 ) , digits = 2 ) [ 1 ] - 2.30 3.14 > signif ( c ( - 2.3 , 3.1415 ) , digits = 2 ) [ 1 ] - 2.3 3.1 > sin ( x) [ 1 ] 0.9589243 0.7568025 - 0.1411200 - 0.9092974 - 0.8414710 0.0000000 0.8414710 0.9092974 0.1411200 - 0.7568025 - 0.9589243 > cos ( x) [ 1 ] 0.2836622 - 0.6536436 - 0.9899925 - 0.4161468 0.5403023 1.0000000 0.5403023 - 0.4161468 - 0.9899925 - 0.6536436 0.2836622
总结:log(x)默认为以常数e为底的自然对数,log10(x)为以10为底的对数,log(16,base = 10)为以10为底的10的对数,exp表示以e为底的指数,ceiling为大于给定值的最小整数,floor为小于给定值的最大整数,trunc为给定值的整数部分,round为给定值四舍五入,默认为整数,如果设定值digits为2,则为保留两个小数。signif和round功能类似,如果digits为2时,表示保留两位有效数字,sin和cos分别为正弦函数和余弦函数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 > vec <- 1: 100 > vec [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [ 31 ] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 [ 61 ] 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 [ 91 ] 91 92 93 94 95 96 97 98 99 100 > sum ( vec) [ 1 ] 5050 > max ( vec) [ 1 ] 100 > min ( vec) [ 1 ] 1 > range ( vec) [ 1 ] 1 100 > mean( vec) [ 1 ] 50.5 > var( vec) [ 1 ] 841.6667 > round ( var( vec) ) [ 1 ] 842 > round ( var( vec) , digits = 2 ) [ 1 ] 841.67 > round ( sd( vec) , digits = 2 ) [ 1 ] 29.01 > prod ( vec) [ 1 ] 9.332622e+157 > quantile( vec) 0 % 25% 50 % 75% 100 % 1.00 25.75 50.50 75.25 100.00 > quantile(vec,c(0.4,0.5,0.8)) 40% 50 % 80% 40.6 50.5 80.2
总结:sum返回向量的求和,max返回向量最大值,min返回向量最小值,range返回向量最小值和最大值,mean返回向量均值,var返回向量方差,sd返回向量标准差,prod返回向量连乘的积。quantile为计算分位数中的值,quantile(vec,c(0.4,0.5,0.8))为计算四分位、中位和八分位数。
1 2 3 4 5 6 7 8 9 10 11 12 13 > t <- c ( 1 , 4 , 2 , 5 , 7 , 9 , 6 ) > t[ 1 ] 1 4 2 5 7 9 6 > which.max( t) [ 1 ] 6 > which.min( t) [ 1 ] 1 > which( t== 7 ) [ 1 ] 5 > which( t> 5 ) [ 1 ] 5 6 7 > t[ which( t> 5 ) ] [ 1 ] 7 9 6
总结:which返回的是对应的位置,which.max(t)返回最大值对应的位置,which.min(t)返回最小值对应的位置,which(t==7)返回数值为7的元素对应的位置,which(t>5)返回t>5对应的元素的位置,t[which(t>5)]返回t>5对应的元素。
2.4 矩阵
矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。向量是一维的,而矩阵是二维的,需要有行和列。
在R软件中,矩阵是有维数的向量,这里的矩阵元素可以是数值型,字符型或者逻辑型,但是每个元素必须都拥有相同的模式,这个和向量一致。
矩阵相关操作如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 > x<- 1 : 20 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > m <- matrix( x, nrow = 4 , ncol = 5 ) > m [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 > t <- matrix( 1 : 20 , 4 , 5 ) > t [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 > t <- matrix( 1 : 20 , 4 ) > t [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 > t <- matrix( 1 : 20 , 4 , byrow = T ) > t [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 2 3 4 5 [ 2 , ] 6 7 8 9 10 [ 3 , ] 11 12 13 14 15 [ 4 , ] 16 17 18 19 20
总结:可以通过matrix创建矩阵,需要自己设定行数或者列数,也可以只设定列数或行数,默认按照列进行排列,如果byrow为T则按照行进行排列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 > m <- matrix( x, nrow = 4 , ncol = 5 ) > m [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 > rnames <- c ( "R1" , "R2" , "R3" , "R4" ) > rnames[ 1 ] "R1" "R2" "R3" "R4" > cnames <- c ( "C1" , "C2" , "C3" , "C4" , "C5" ) > cnames[ 1 ] "C1" "C2" "C3" "C4" "C5" > dimnames ( m) <- list ( rnames, cnames) > m C1 C2 C3 C4 C5 R1 1 5 9 13 17 R2 2 6 10 14 18 R3 3 7 11 15 19 R4 4 8 12 16 20 > x <- 1: 20 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > dim ( x) NULL > dim ( x) <- c ( 4 , 5 ) > x [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20
总结:可以通过dimnames给矩阵的行和列进行命名,也可以通过dim将向量变为矩阵。
数组:示例1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > x <- 1: 20 > dim ( x) NULL > dim ( x) <- c ( 2 , 2 , 5 ) > x, , 1 [ , 1 ] [ , 2 ] [ 1 , ] 1 3 [ 2 , ] 2 4 , , 2 [ , 1 ] [ , 2 ] [ 1 , ] 5 7 [ 2 , ] 6 8 , , 3 [ , 1 ] [ , 2 ] [ 1 , ] 9 11 [ 2 , ] 10 12 , , 4 [ , 1 ] [ , 2 ] [ 1 , ] 13 15 [ 2 , ] 14 16 , , 5 [ , 1 ] [ , 2 ] [ 1 , ] 17 19 [ 2 , ] 18 20
示例2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 > dim1 <- c ( "A1" , "A2" ) > dim2 <- c ( "B1" , "B2" , "B3" ) > dim3 <- c ( "C1" , "C2" , "C3" , "C4" ) > z <- array( 1 : 24 , c ( 2 , 3 , 4 ) , dimnames = list ( dim1, dim2, dim3) ) > z, , C1 B1 B2 B3 A1 1 3 5 A2 2 4 6 , , C2 B1 B2 B3 A1 7 9 11 A2 8 10 12 , , C3 B1 B2 B3 A1 13 15 17 A2 14 16 18 , , C4 B1 B2 B3 A1 19 21 23 A2 20 22 24
总结:可以通过array创建矩阵,同时给矩阵命名。
读取矩阵中的元素,示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 > m <- matrix( 1 : 20 , 4 , 5 , byrow = T ) > m [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 2 3 4 5 [ 2 , ] 6 7 8 9 10 [ 3 , ] 11 12 13 14 15 [ 4 , ] 16 17 18 19 20 > m[ 1 , 2 ] [ 1 ] 2 > m[ 1 , c ( 2 , 3 , 4 ) ] [ 1 ] 2 3 4 > m[ c ( 2 : 4 ) , c ( 2 , 3 ) ] [ , 1 ] [ , 2 ] [ 1 , ] 7 8 [ 2 , ] 12 13 [ 3 , ] 17 18 > m[ 2 , ] [ 1 ] 6 7 8 9 10 > m[ , 2 ] [ 1 ] 2 7 12 17 > m[ 2 ] [ 1 ] 6 > m[ 3 ] [ 1 ] 11 > m[ - 1 , 2 ] [ 1 ] 7 12 17 > rnames <- c ( "R1" , "R2" , "R3" , "R4" ) > rnames[ 1 ] "R1" "R2" "R3" "R4" > cnames <- c ( "C1" , "C2" , "C3" , "C4" , "C5" ) > cnames[ 1 ] "C1" "C2" "C3" "C4" "C5" > dimnames ( m) = list ( rnames, cnames) > m C1 C2 C3 C4 C5 R1 1 2 3 4 5 R2 6 7 8 9 10 R3 11 12 13 14 15 R4 16 17 18 19 20 > m[ "R1" , "C2" ] [ 1 ] 2 sum ( m) [ 1 ] 210 > colSums( m) C1 C2 C3 C4 C5 34 38 42 46 50 > rowSums( m) R1 R2 R3 R4 15 40 65 90 > colMeans( m) C1 C2 C3 C4 C5 8.5 9.5 10.5 11.5 12.5 > rowMeans( m) R1 R2 R3 R4 3 8 13 18
矩阵的内积和外积:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 > n <- matrix( 1 : 9 , 3 , 3 ) > w <- matrix( 2 : 10 , 3 , 3 ) > n [ , 1 ] [ , 2 ] [ , 3 ] [ 1 , ] 1 4 7 [ 2 , ] 2 5 8 [ 3 , ] 3 6 9 > w [ , 1 ] [ , 2 ] [ , 3 ] [ 1 , ] 2 5 8 [ 2 , ] 3 6 9 [ 3 , ] 4 7 10 > n* w [ , 1 ] [ , 2 ] [ , 3 ] [ 1 , ] 2 20 56 [ 2 , ] 6 30 72 [ 3 , ] 12 42 90 > n %*% w [ , 1 ] [ , 2 ] [ , 3 ] [ 1 , ] 42 78 114 [ 2 , ] 51 96 141 [ 3 , ] 60 114 168 > diag( n) [ 1 ] 1 5 9 > t( n) [ , 1 ] [ , 2 ] [ , 3 ] [ 1 , ] 1 2 3 [ 2 , ] 4 5 6 [ 3 , ] 7 8 9
总结:函数内积可通过*将矩阵对应位置进行相乘,外积可以通过%*%符号实现,矩阵对角线的值可以通过diag取得,函数t可以对矩阵进行转置。
2.5 列表
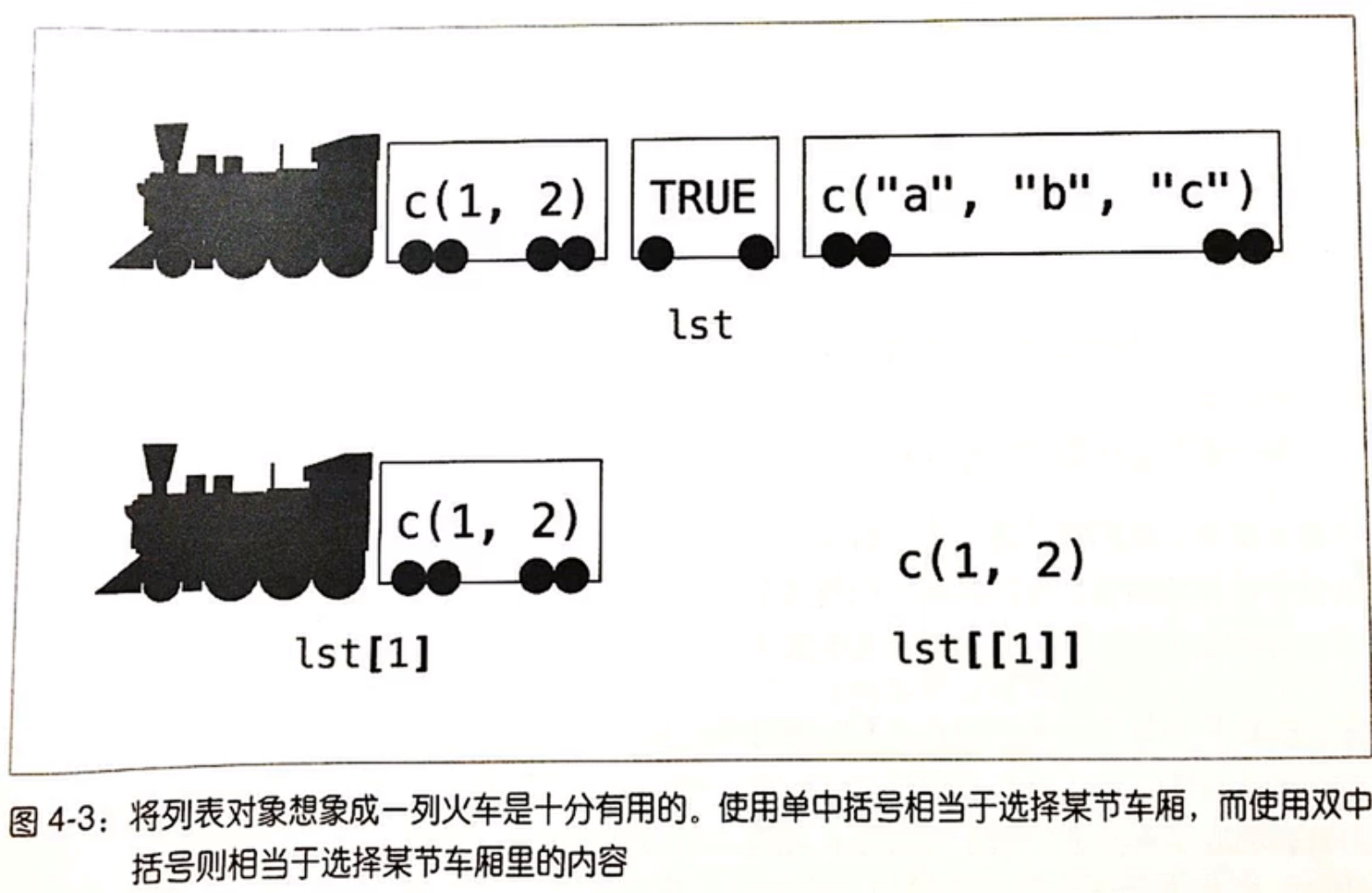
列表就是用来存储很多内容的一个集合,在其他编程语言中,列表一般和数组是等同的,但是在R语言中,列表却是最复杂的一种数据结构,也是非常重要的一种数据结构。
列表是一些对象的有序集合。列表中可以存储若干向量、矩阵、数据框,甚至其他列表的组合。
向量与类表:
在模式上和向量类似,都是一维数据集合。
向量智能存储一种数据类型,列表中的对象可以是R中的任何数据结构,甚至列表本身。
示例:mtcars为数据集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 > a <- 1: 20 > b <- matrix( 1 : 20 , 4 ) > c <- mtcars> d <- "This is a test list" > mlist<- list ( a, b, c , d) > mlist[[ 1 ] ] [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [[ 2 ] ] [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 [[ 3 ] ] mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 [[ 4 ] ] [ 1 ] "This is a test list" > mlist <- list ( first= a, second= b, third= c , forth= d) > mlist$ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 $ second [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 $ third mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 $ forth[ 1 ] "This is a test list" > mlist[ 1 ] $ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > mlist[ c ( 1 , 4 ) ] $ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 $ forth[ 1 ] "This is a test list"
总结:可以通过以上的方式进行命名,并根据需要输出相关内容。
1 2 3 4 5 6 7 8 9 10 11 12 13 > state.center[ c ( "x" , "y" ) ] $ x [ 1 ] - 86.7509 - 127.2500 - 111.6250 - 92.2992 - 119.7730 - 105.5130 - 72.3573 - 74.9841 - 81.6850 - 83.3736 - 126.2500 - 113.9300 [ 13 ] - 89.3776 - 86.0808 - 93.3714 - 98.1156 - 84.7674 - 92.2724 - 68.9801 - 76.6459 - 71.5800 - 84.6870 - 94.6043 - 89.8065 [ 25 ] - 92.5137 - 109.3200 - 99.5898 - 116.8510 - 71.3924 - 74.2336 - 105.9420 - 75.1449 - 78.4686 - 100.0990 - 82.5963 - 97.1239 [ 37 ] - 120.0680 - 77.4500 - 71.1244 - 80.5056 - 99.7238 - 86.4560 - 98.7857 - 111.3300 - 72.5450 - 78.2005 - 119.7460 - 80.6665 [ 49 ] - 89.9941 - 107.2560 $ y [ 1 ] 32.5901 49.2500 34.2192 34.7336 36.5341 38.6777 41.5928 38.6777 27.8744 32.3329 31.7500 43.5648 40.0495 40.0495 41.9358 [ 16 ] 38.4204 37.3915 30.6181 45.6226 39.2778 42.3645 43.1361 46.3943 32.6758 38.3347 46.8230 41.3356 39.1063 43.3934 39.9637 [ 31 ] 34.4764 43.1361 35.4195 47.2517 40.2210 35.5053 43.9078 40.9069 41.5928 33.6190 44.3365 35.6767 31.3897 39.1063 44.2508 [ 46 ] 37.5630 47.4231 38.4204 44.5937 43.0504
总结:可以通过命名提取相应的列表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > mlist$ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > mlist[ 1 ] $ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > mlist[[ 1 ] ] [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > class ( mlist[[ 1 ] ] ) [ 1 ] "integer" > class ( mlist[ 1 ] ) [ 1 ] "list"
总结:可以通过class查看数据类型,mlist[1]和mlist[[1]]是不同的数据类型。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > mlist <- mlist[ - 3 ] > mlist$ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 $ second [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ 1 , ] 1 5 9 13 17 [ 2 , ] 2 6 10 14 18 [ 3 , ] 3 7 11 15 19 [ 4 , ] 4 8 12 16 20 $ forth[ 1 ] "This is a test list" > mlist[ 2 ] <- NULL > mlist$ first [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 $ forth[ 1 ] "This is a test list"
总结:可以通过负号去掉不需要的部分,然后赋值给自身,这样可以删除部分列表内容。或者给相应的列表置空。first、second和forth只是名称并不代表相应的顺序。
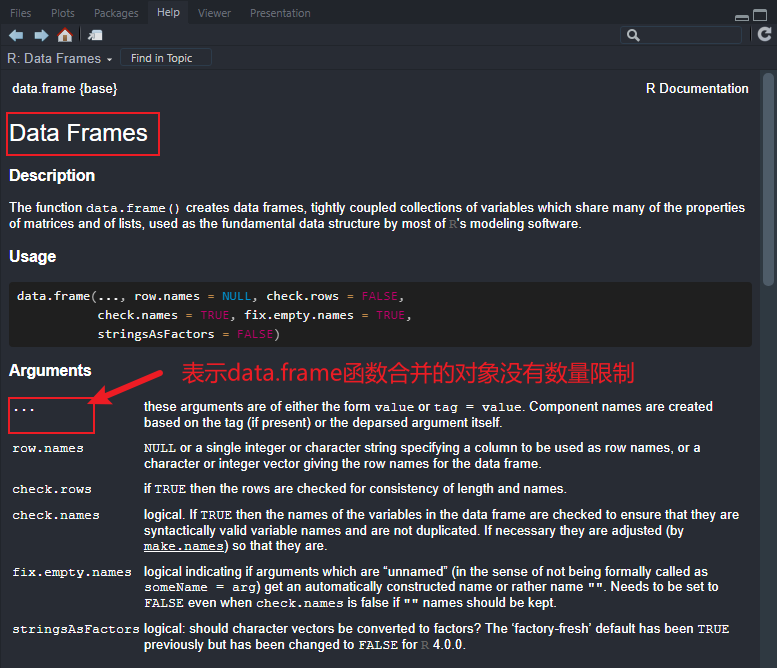
2.6 数据框
数据框是一种表格式的数据结构。数据框旨在模拟数据集,与其他统计软件如SAS或者SPSS中的数据集的概念一致。
数据集通常是由数据构成的一个矩形数组,行表示观测,列表示变量。不同的行业对于数据集的行和列的叫法不同。
数据框实际上是一个列表,列表中的元素是向量,这些向量构成数据框的列,每一列必须具有相同的长度,所以数据框是矩形结构,而且数据框的列必须命名。
矩阵和数据框:
数据框形状上很像矩阵;
数据框是比较规则的列表;
矩阵必须为同一数据类型;
数据框每一列必须同一类型,每一行可以不同。
1 2 > state <- data.frame( state.name, state.abb, state.region, state.x77) > state
总结:通过data.frame将向量组成数据框。
1 2 3 4 state[ c ( 2 , 4 ) ] state[ , "state.abb" ] state[ "Alabama" , ] state$ state.abb
总结:通过以上方式可以提取相关行或列中的数据。
示例:
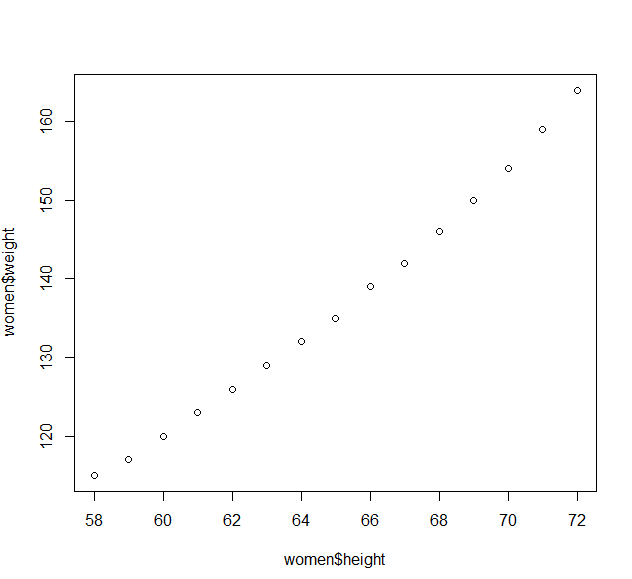
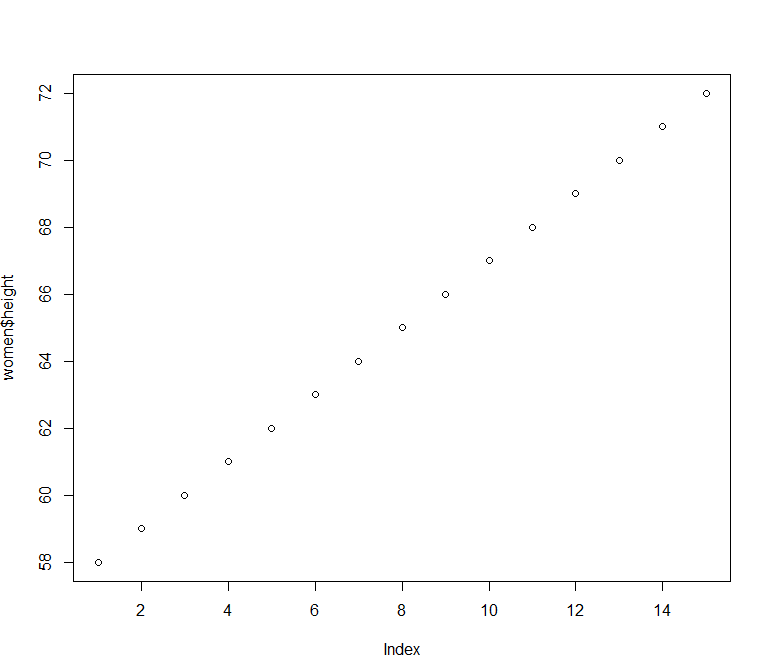
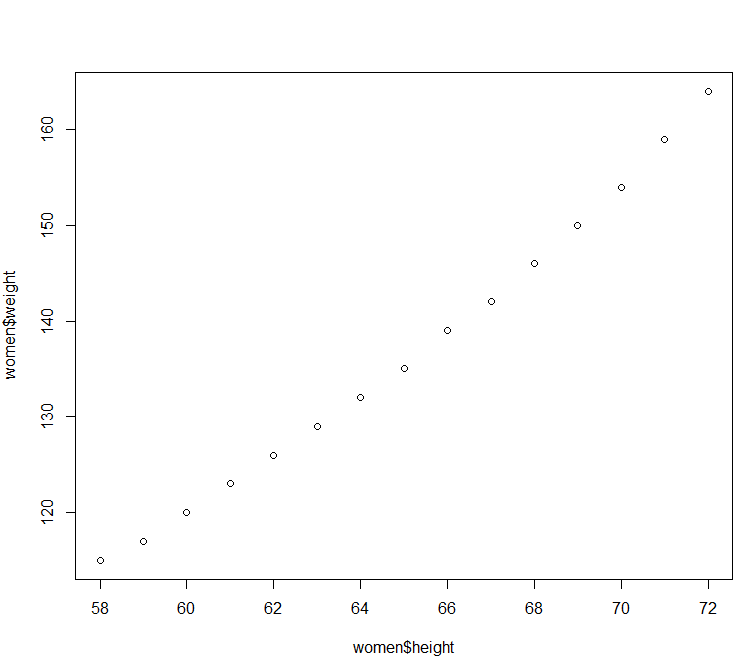
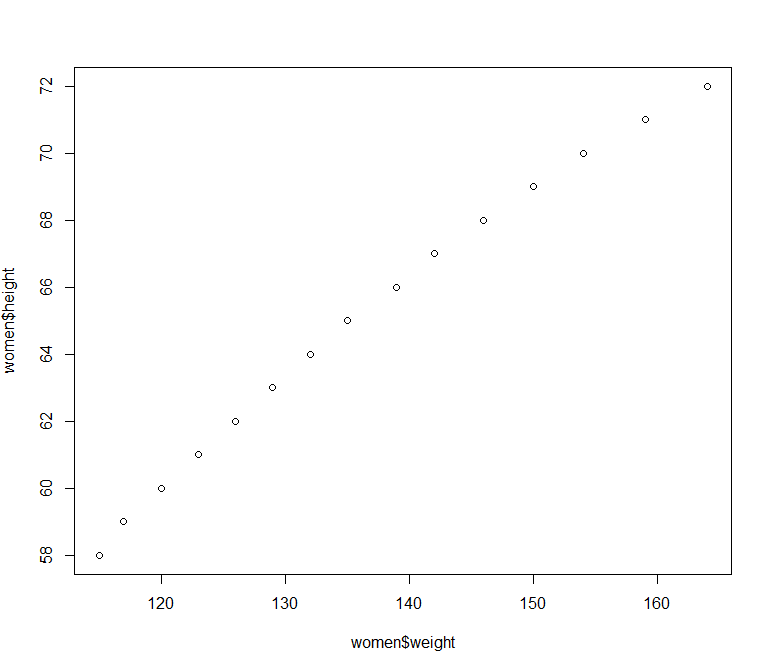
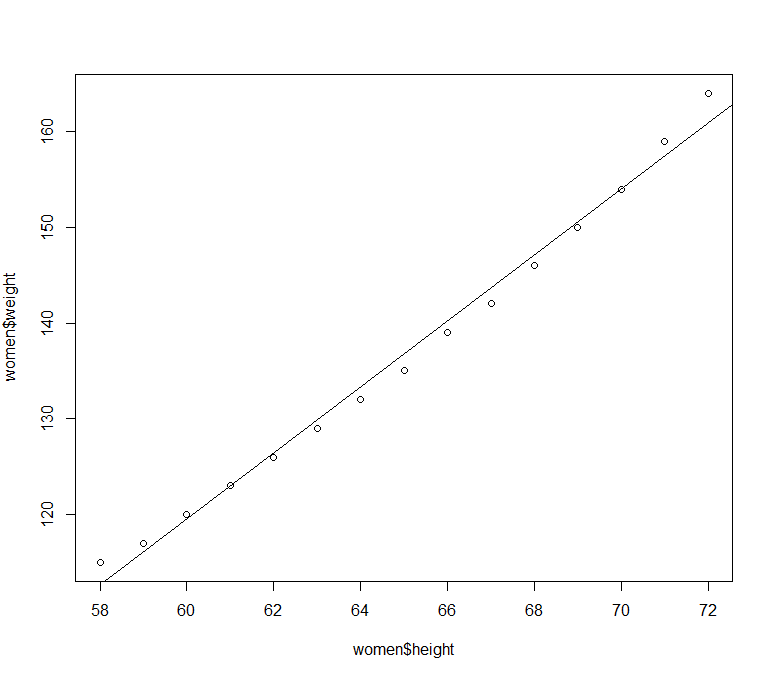
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > women height weight 1 58 115 2 59 117 3 60 120 4 61 123 5 62 126 6 63 129 7 64 132 8 65 135 9 66 139 10 67 142 11 68 146 12 69 150 13 70 154 14 71 159 15 72 164 > plot( women$ height, women$ weight)
运行结果:
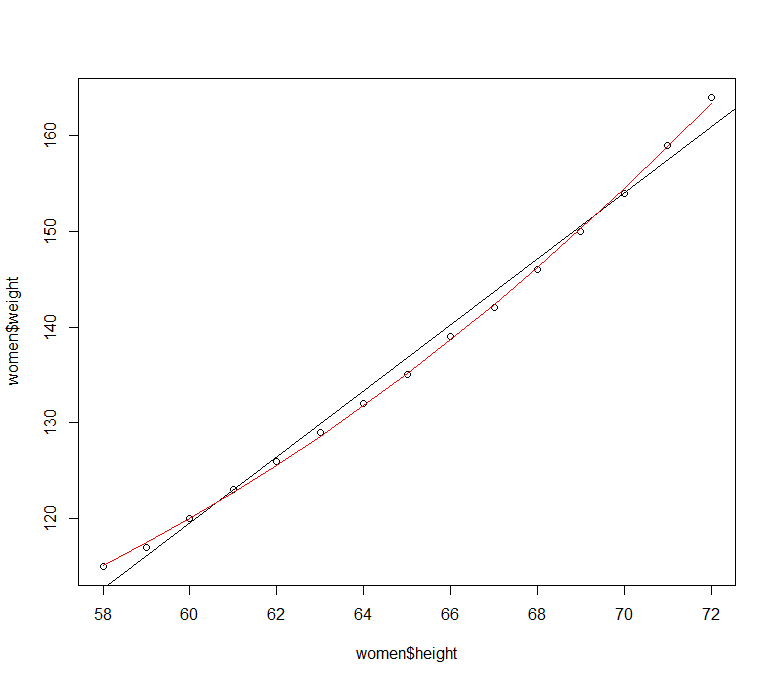
在lm函数进行线性回归的时候,直接给出列名即可:
1 2 3 4 5 6 7 8 > lm( height~ weight, data = women) Call: lm( formula = height ~ weight, data = women) Coefficients: ( Intercept) weight 25.7235 0.2872
R语言中提供了attach函数,将数据框加载到搜索框中,不需要再使用$符号,直接输入列的名字即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > attach( mtcars) > mpg [ 1 ] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 [ 25 ] 19.2 27.3 26.0 30.4 15.8 19.7 15.0 21.4 > colnames( mtcars) [ 1 ] "mpg" "cyl" "disp" "hp" "drat" "wt" "qsec" "vs" "am" "gear" "carb" > rownames( mtcars) [ 1 ] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" "Hornet Sportabout" [ 6 ] "Valiant" "Duster 360" "Merc 240D" "Merc 230" "Merc 280" [ 11 ] "Merc 280C" "Merc 450SE" "Merc 450SL" "Merc 450SLC" "Cadillac Fleetwood" [ 16 ] "Lincoln Continental" "Chrysler Imperial" "Fiat 128" "Honda Civic" "Toyota Corolla" [ 21 ] "Toyota Corona" "Dodge Challenger" "AMC Javelin" "Camaro Z28" "Pontiac Firebird" [ 26 ] "Fiat X1-9" "Porsche 914-2" "Lotus Europa" "Ford Pantera L" "Ferrari Dino" [ 31 ] "Maserati Bora" "Volvo 142E" > detach( mtcars)
也可以使用with实现数据集的调用:
1 2 3 4 5 6 7 8 9 10 > with( mtcars, { hp} ) [ 1 ] 110 110 93 110 175 105 245 62 95 123 123 180 180 180 205 215 230 66 52 65 97 150 150 245 175 66 91 113 264 175 [ 31 ] 335 109 > with( mtcars, { mpg} ) [ 1 ] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 [ 25 ] 19.2 27.3 26.0 30.4 15.8 19.7 15.0 21.4 > with( mtcars, { sum ( mpg) } ) [ 1 ] 642.9
单双中括号的区别:
2.7 因子
变量分类:
名义型变量
有序型变量
连续型变量
因子:在R中名义型变量和有序型变量称为因子,factor。这些分类变量的可能值成为一个水平,level,例如good、better、better,都称为一个level。由这些水平值构成的向量就称为因子。因子本身也是一个向量,一个集合,只不过里面的元素可以用来分类。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > mtcars mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 > mtcars$ cyl [ 1 ] 6 6 4 6 8 6 8 4 4 6 6 8 8 8 8 8 8 4 4 4 4 8 8 8 8 4 4 4 8 6 8 4 > table( mtcars$ cyl) 4 6 8 11 7 14 > table( mtcars$ am) 0 1 19 13
总结:上面的4、6、8并不是因子,而是cyl这一列可以当作因子类型来处理,4、6或8为一个level。使用table函数进行频数统计。
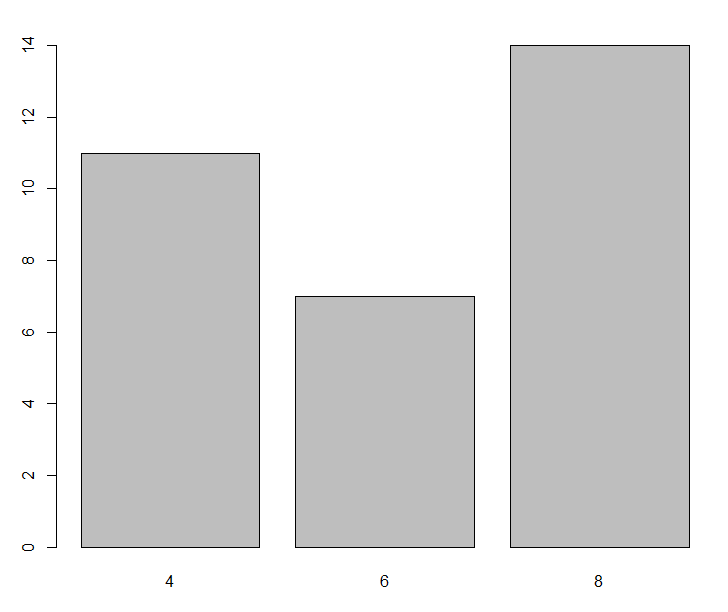
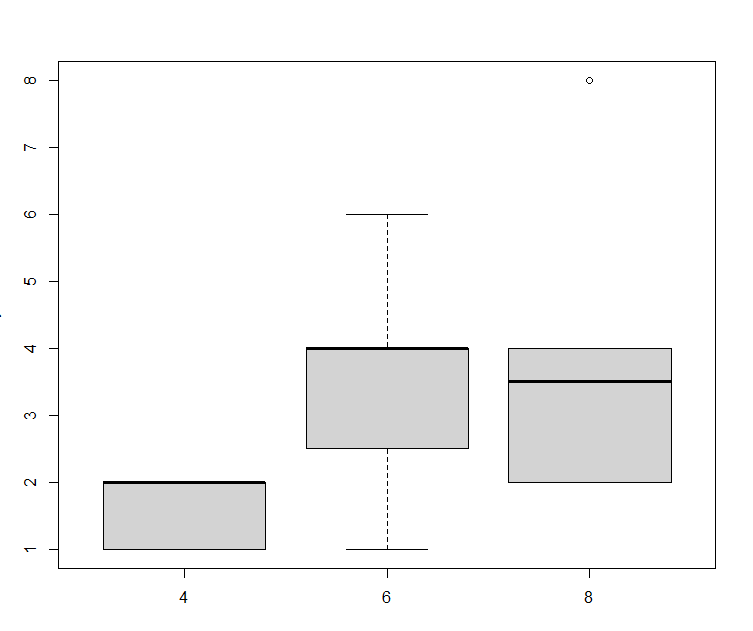
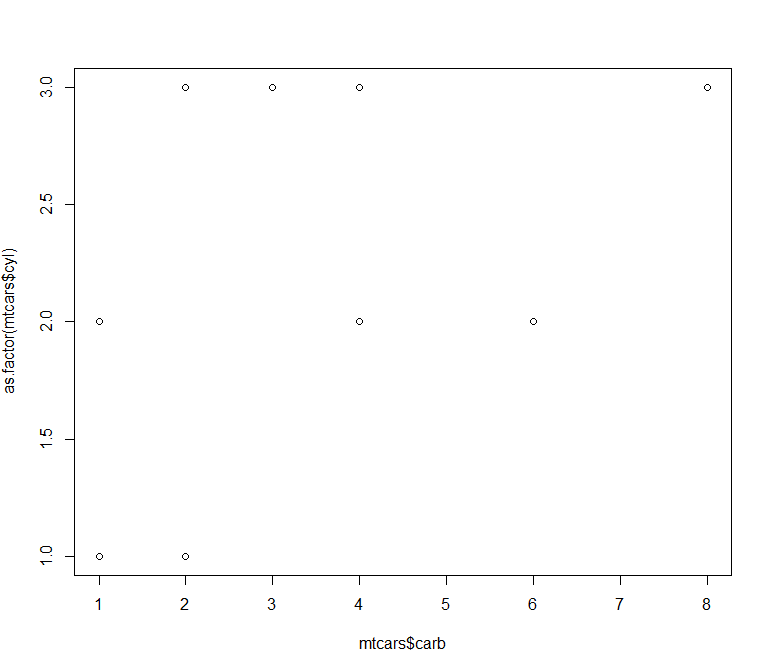
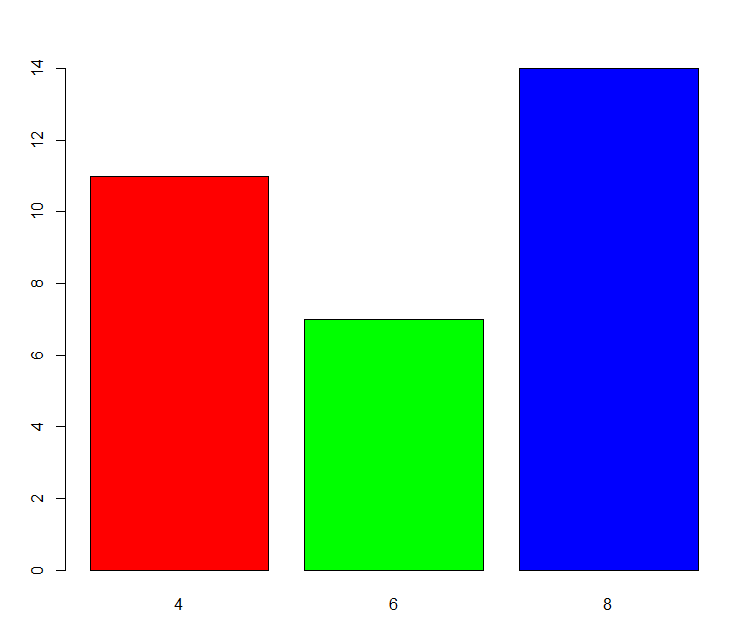
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > f <- factor( c ( "red" , "red" , "green" , "blue" , "green" , "blue" , "blue" ) ) > f[ 1 ] red red green blue green blue blue Levels: blue green red > week <- factor( c ( "Mon" , "Fri" , "Thu" , "Wed" , "Mon" , "Fri" , "Sun" ) ) > week[ 1 ] Mon Fri Thu Wed Mon Fri SunLevels: Fri Mon Sun Thu Wed > week <- factor( c ( "Mon" , "Fri" , "Thu" , "Wed" , "Mon" , "Fri" , "Sun" ) , ordered = T , levels = c ( "Mon" , "Tue" , "Wed" , "Thu" , "Fri" , "Sat" , "Sun" ) ) > week[ 1 ] Mon Fri Thu Wed Mon Fri SunLevels: Mon < Tue < Wed < Thu < Fri < Sat < Sun > fcyl <- factor( mtcars$ cyl) > fcyl [ 1 ] 6 6 4 6 8 6 8 4 4 6 6 8 8 8 8 8 8 4 4 4 4 8 8 8 8 4 4 4 8 6 8 4 Levels: 4 6 8 > plot( mtcars$ cyl) > plot( factor( mtcars$ cyl) )
总结:可以通过factor创建因子类型。有序型变量也可以作为因子。fcyl <- factor(mtcars$cyl)可以将cyl向量变为因子。向量输出的是散点图,而因子输出的是条形图。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > num <- 1: 100 > num [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [ 31 ] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 [ 61 ] 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 [ 91 ] 91 92 93 94 95 96 97 98 99 100 > cut( num, c ( seq( 0 , 100 , 10 ) ) ) [ 1 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 0 , 10 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] [ 14 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] [ 27 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] [ 40 ] ( 30 , 40 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 40 , 50 ] ( 50 , 60 ] ( 50 , 60 ] [ 53 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 50 , 60 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] [ 66 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] ( 60 , 70 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] ( 70 , 80 ] [ 79 ] ( 70 , 80 ] ( 70 , 80 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 80 , 90 ] ( 90 , 100 ] [ 92 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] ( 90 , 100 ] Levels: ( 0 , 10 ] ( 10 , 20 ] ( 20 , 30 ] ( 30 , 40 ] ( 40 , 50 ] ( 50 , 60 ] ( 60 , 70 ] ( 70 , 80 ] ( 80 , 90 ] ( 90 , 100 ] > class ( cut( num, c ( seq( 0 , 100 , 10 ) ) ) ) [ 1 ] "factor"
通过cut可以统计每个区间分别有多少。
2.8 缺失数据
缺失数据的分类
统计学家通常将缺失数据分为三类。它们都用概率术语进行描述,但思想都非常直观。我们将用sleep研究中对做梦时长的测量(有12个动物有缺失值)来依次阐述三种类型。
完全随机缺失若某变量的缺失数据与其他任何观测或未观测变量都不相关,则数据为完全随机缺失(MCAR)。若12个动物的做梦时长值缺失不是由于系统原因,那么可认为数据是MCAR。注意,如果每个有缺失值的变量都是MCAR,那么可以将数据完整的实例看做是对更大数据集的一个简单随机抽样。
随机缺失若某变量上的缺失数据与其他观测变量相关,与它自己的未观测值不相关,则数据为随机缺失(MAR)。例如,体重较小的动物更可能有做梦时长的缺失值(可能因为较小的动物较难观察),“缺失”与动物的做梦时长无关,那么该数据就可以认为是MAR。
非随机缺失若缺失数据不属于MCAR或MAR,则数据为非随机缺失(NMAR)。例如,做梦时长越短的动物也更可能有做梦数据的缺失(可能由于难以测量时长较短的事件),那么数据可认为是NMAR。
为何会出现缺失数据:
机器断电,设备故障导致某个测量值发生了丢失。
测量根本没有发生,例如在做调查问卷时,有些问题没有回答,或者有些问题是无效回答等。
缺失值NA
在R中,NA代表缺失值,NA是不可用,not available的简称,用来存储缺失信息。
这里缺失值NA表示没有,但注意没有并不一定就是0,NA是不知道是多少,也能是0,也可能是任何值,缺失值和值为0是完全不同的。
1 2 3 4 > 1 + NA [ 1 ] NA > NA == 0 [ 1 ] NA
在运行中NA的处理:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > a <- c ( NA , 1 : 49 ) > a [ 1 ] NA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 [ 42 ] 41 42 43 44 45 46 47 48 49 > sum ( a) [ 1 ] NA > mean( a) [ 1 ] NA > sum ( a, na.rm = TRUE ) [ 1 ] 1225 > mean( a, na.rm = TRUE ) [ 1 ] 25 > mean( 1 : 49 ) [ 1 ] 25 > is.na ( a) [ 1 ] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [ 21 ] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [ 41 ] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
总结:可以通过na.rm将NA进行剔除,剔除后,不会将NA的位置保留进行计算。通过is.na判断是否存在NA。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 > c [ 1 ] NA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 NA NA > d <- na.omit( c ) > d [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 attr ( , "na.action" ) [ 1 ] 1 22 23 attr ( , "class" ) [ 1 ] "omit" > is.na ( d) [ 1 ] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE > sum ( d) [ 1 ] 210 > mean( d) [ 1 ] 10.5 > na.omit( sleep) BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger 2 1.000 6.60 6.3 2.0 8.3 4.5 42.0 3 1 3 5 2547.000 4603.00 2.1 1.8 3.9 69.0 624.0 3 5 4 6 10.550 179.50 9.1 0.7 9.8 27.0 180.0 4 4 4 7 0.023 0.30 15.8 3.9 19.7 19.0 35.0 1 1 1 8 160.000 169.00 5.2 1.0 6.2 30.4 392.0 4 5 4 ... 57 0.900 2.60 11.0 2.3 13.3 4.5 60.0 2 1 2 58 2.000 12.30 4.9 0.5 5.4 7.5 200.0 3 1 3 59 0.104 2.50 13.2 2.6 15.8 2.3 46.0 3 2 2 60 4.190 58.00 9.7 0.6 10.3 24.0 210.0 4 3 4 61 3.500 3.90 12.8 6.6 19.4 3.0 14.0 2 1 1
总结:可以通过na.omit(sleep)将数据框中的NA对应的这一行的数据删除。
1 2 3 4 > length ( rownames( sleep) ) [ 1 ] 62 > length ( rownames( na.omit( sleep) ) ) [ 1 ] 42
但是这样也会出现问题,比如NA占据的行数有一半,则会导致大量数据丢失,影响分析结果。
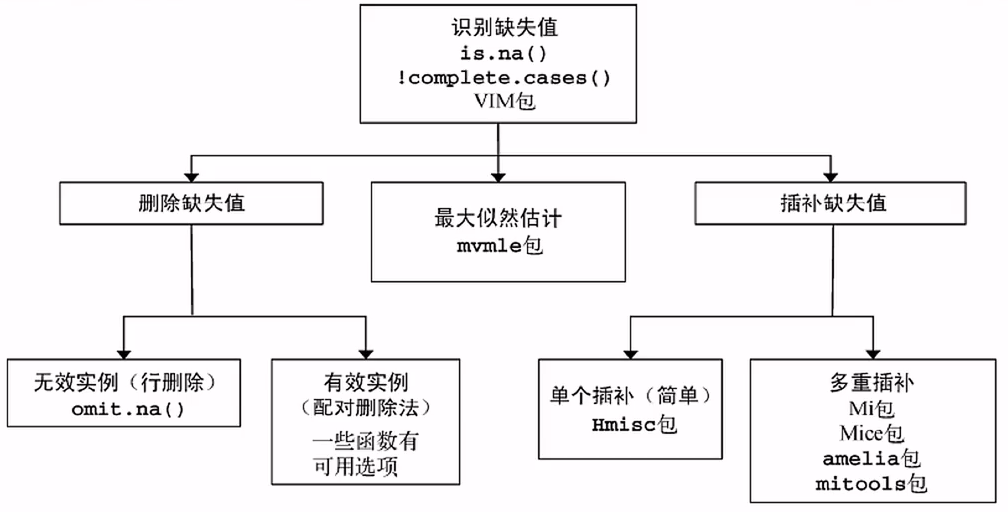
R提供了多种处理缺失值的方法:
其他缺失数据:
缺失数据NaN,代表不可能的值;
Inf代表无穷,分为正无穷Inf和负无穷-Inf,代表无穷大或者无穷小。
不同缺失值之间的差别:
NA是存在的值,但是不知道是多少;
NaN是不存在的;
Inf存在,是无穷大或者无穷小,但是表示不可能的值。
1 2 3 4 5 6 7 8 9 10 11 12 > 1 / 0 [ 1 ] Inf > - 1 / 0 [ 1 ] - Inf > 0 / 0 [ 1 ] NaN > is.nan ( 0 / 0 ) [ 1 ] TRUE > is.infinite ( 1 / 0 ) [ 1 ] TRUE > is.infinite ( - 1 / 0 ) [ 1 ] TRUE
2.9 字符串
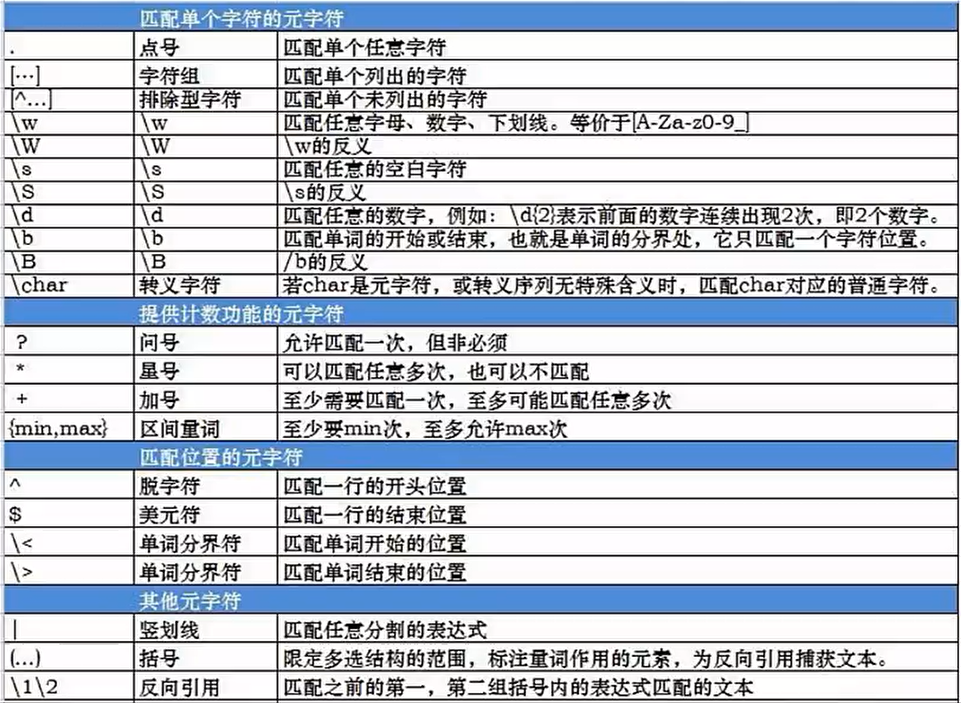
R语言支持正则表达式,正则表达式如下:
下面介绍处理字符串的函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > nchar( "hello world" ) [ 1 ] 11 > month.name [ 1 ] "January" "February" "March" "April" "May" "June" "July" "August" "September" "October" [ 11 ] "November" "December" > nchar( month.name ) [ 1 ] 7 8 5 5 3 4 4 6 9 7 8 8 > length ( month.name ) [ 1 ] 12 > nchar( c ( 12 , 2 , 345 ) ) [ 1 ] 2 1 3 > paste( "Everybody" , "loves" , "stats" ) [ 1 ] "Everybody loves stats" > paste( "Everybody" , "loves" , "stats" , sep = "-" ) [ 1 ] "Everybody-loves-stats" > names <- c ( "Moe" , "Larry" , "Curly" ) > paste( names , "loves stats" ) [ 1 ] "Moe loves stats" "Larry loves stats" "Curly loves stats"
总结:nchar可以用来统计字符数,空格也算一个字符。length计算的是元素的个数,而nchar计算的是每个元素字符的长度。paste是将多个字符串连成一个字符串,通过空格进行连接,也可以通过sep设定连接符,也可以将多个字符串分别和某一个固定的字符串进行连接。
1 2 3 4 5 6 7 8 9 10 11 12 13 > substr( x = month.name , start = 1 , stop = 3 ) [ 1 ] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec" > temp <- substr( x = month.name , start = 1 , stop = 3 ) > toupper( temp) [ 1 ] "JAN" "FEB" "MAR" "APR" "MAY" "JUN" "JUL" "AUG" "SEP" "OCT" "NOV" "DEC" > tolower( temp) [ 1 ] "jan" "feb" "mar" "apr" "may" "jun" "jul" "aug" "sep" "oct" "nov" "dec" > gsub( "^(\\w)" , "\\U\\1" , tolower( temp) , perl = T ) [ 1 ] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec" > gsub( "^(\\w)" , "\\L\\1" , tolower( temp) , perl = T ) [ 1 ] "jan" "feb" "mar" "apr" "may" "jun" "jul" "aug" "sep" "oct" "nov" "dec" > gsub( "^(\\w)" , "\\L\\1" , toupper( temp) , perl = T ) [ 1 ] "jAN" "fEB" "mAR" "aPR" "mAY" "jUN" "jUL" "aUG" "sEP" "oCT" "nOV" "dEC"
总结:字符串分隔符substr可以进行字符串分割,sub进行一次字符替换,而gsub可以进行全局替换,需要使用正则表达式进行操作。
1 2 3 4 5 6 7 8 9 > x <- c ( "b" , "A+" , "AC" ) > x[ 1 ] "b" "A+" "AC" > grep( "A+" , x) [ 1 ] 2 3 > grep( "A+" , x, fixed = T ) [ 1 ] 2 > grep( "A+" , x, fixed = F ) [ 1 ] 2 3
总结:grep可以用来查找字符串,如果grep参数中fixed为T,则不支持正则表达式,返回值为匹配的下标,grep支持正则表达式,如果Fixed为F,则支持正则表达式,其中A+中的+号表示所有字符。
1 2 3 4 5 > x <- c ( "b" , "A+" , "AC" ) > x[ 1 ] "b" "A+" "AC" > match( "AC" , x) [ 1 ] 3
总结:match也可以进行字符串匹配,但是不支持正则表达式,没有grep强大。
1 2 3 4 5 6 7 8 9 10 > path <- "/use/local/bin/R" > strsplit( path, "/" ) [[ 1 ] ] [ 1 ] "" "use" "local" "bin" "R" > strsplit( c ( path, path) , "/" ) [[ 1 ] ] [ 1 ] "" "use" "local" "bin" "R" [[ 2 ] ] [ 1 ] "" "use" "local" "bin" "R"
总结:strsplit为字符串分割函数,需要指定分隔符,在上面的例子中,分隔符为/。strsplit返回的值是一个列表而不是一个向量。可以同时处理分割多个字符串,也方便后面的处理。
许多函数都有fixed参数设置,表示是否支持正则表达式,使用正则表达式很方便进行处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 face <- 1: 13 suit <- c ( "spades" , "clubs" , "hearts" , "diamonds" ) > outer( suit, face, FUN= paste) [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ , 6 ] [ , 7 ] [ , 8 ] [ , 9 ] [ 1 , ] "spades 1" "spades 2" "spades 3" "spades 4" "spades 5" "spades 6" "spades 7" "spades 8" "spades 9" [ 2 , ] "clubs 1" "clubs 2" "clubs 3" "clubs 4" "clubs 5" "clubs 6" "clubs 7" "clubs 8" "clubs 9" [ 3 , ] "hearts 1" "hearts 2" "hearts 3" "hearts 4" "hearts 5" "hearts 6" "hearts 7" "hearts 8" "hearts 9" [ 4 , ] "diamonds 1" "diamonds 2" "diamonds 3" "diamonds 4" "diamonds 5" "diamonds 6" "diamonds 7" "diamonds 8" "diamonds 9" [ , 10 ] [ , 11 ] [ , 12 ] [ , 13 ] [ 1 , ] "spades 10" "spades 11" "spades 12" "spades 13" [ 2 , ] "clubs 10" "clubs 11" "clubs 12" "clubs 13" [ 3 , ] "hearts 10" "hearts 11" "hearts 12" "hearts 13" [ 4 , ] "diamonds 10" "diamonds 11" "diamonds 12" "diamonds 13" > outer( suit, face, FUN= paste, sep = "-" ) [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ , 6 ] [ , 7 ] [ , 8 ] [ , 9 ] [ 1 , ] "spades-1" "spades-2" "spades-3" "spades-4" "spades-5" "spades-6" "spades-7" "spades-8" "spades-9" [ 2 , ] "clubs-1" "clubs-2" "clubs-3" "clubs-4" "clubs-5" "clubs-6" "clubs-7" "clubs-8" "clubs-9" [ 3 , ] "hearts-1" "hearts-2" "hearts-3" "hearts-4" "hearts-5" "hearts-6" "hearts-7" "hearts-8" "hearts-9" [ 4 , ] "diamonds-1" "diamonds-2" "diamonds-3" "diamonds-4" "diamonds-5" "diamonds-6" "diamonds-7" "diamonds-8" "diamonds-9" [ , 10 ] [ , 11 ] [ , 12 ] [ , 13 ] [ 1 , ] "spades-10" "spades-11" "spades-12" "spades-13" [ 2 , ] "clubs-10" "clubs-11" "clubs-12" "clubs-13" [ 3 , ] "hearts-10" "hearts-11" "hearts-12" "hearts-13" [ 4 , ] "diamonds-10" "diamonds-11" "diamonds-12" "diamonds-13"
总结:outer函数可以生成两个字符串的所有组合,两个字符串的连接默认通过空格的形式,也可以自定义连接符。
2.10 日期和时间
时间序列分析:
对时间序列的描述;
利用前面的结果进行预测。
时间序列包:TimeSeries
时间数据集:sunspots、presidents、airmiles
1 2 > class ( presidents) [ 1 ] "ts"
总结:这里的ts表示时间序列,有些数据集是时间序列数据,但是数据形式是数据框。
1 2 3 4 5 6 7 8 9 10 11 > Sys.Date( ) [ 1 ] "2022-08-06" > class ( Sys.Date( ) ) [ 1 ] "Date" > a <- "2017-01-01" > a[ 1 ] "2017-01-01" > as.Date( a, format = "%Y-%m-%d" ) [ 1 ] "2017-01-01" > class ( as.Date( a, format = "%Y-%m-%d" ) ) [ 1 ] "Date"
总结:Sys.Date函数可以查看当前的年月日,Sys.Date()中的数据类型为Date类型,可以通过as.Date函数将字符串类型转换成Date类型。
更多格式化参数,可以通过?strftime命令参看strftime函数中的介绍。
1 2 3 4 5 > seq( as.Date( "2017-01-01" ) , as.Date( "2017-06-23" ) , by = 5 ) [ 1 ] "2017-01-01" "2017-01-06" "2017-01-11" "2017-01-16" "2017-01-21" "2017-01-26" "2017-01-31" "2017-02-05" "2017-02-10" [ 10 ] "2017-02-15" "2017-02-20" "2017-02-25" "2017-03-02" "2017-03-07" "2017-03-12" "2017-03-17" "2017-03-22" "2017-03-27" [ 19 ] "2017-04-01" "2017-04-06" "2017-04-11" "2017-04-16" "2017-04-21" "2017-04-26" "2017-05-01" "2017-05-06" "2017-05-11" [ 28 ] "2017-05-16" "2017-05-21" "2017-05-26" "2017-05-31" "2017-06-05" "2017-06-10" "2017-06-15" "2017-06-20"
总结:可以使用seq函数创建连续的时间点,by表示间隔五天。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > sales <- round ( runif( 48 , min = 50 , max = 100 ) ) > sales [ 1 ] 56 88 87 91 83 82 90 68 100 64 64 62 85 51 76 91 53 94 80 93 77 73 53 59 88 71 98 89 74 66 [ 31 ] 91 57 71 50 67 91 70 60 51 71 99 73 95 52 57 72 82 72 > ts( sales, start = c ( 2010 , 5 ) , end = c ( 2014 , 4 ) , frequency = 1 ) Time Series: Start = 2014 End = 2017 Frequency = 1 [ 1 ] 56 88 87 91 > ts( sales, start = c ( 2010 , 5 ) , end = c ( 2014 , 4 ) , frequency = 4 ) Qtr1 Qtr2 Qtr3 Qtr4 2011 56 88 87 91 2012 83 82 90 68 2013 100 64 64 62 2014 85 51 76 91 > ts( sales, start = c ( 2010 , 5 ) , end = c ( 2014 , 4 ) , frequency = 12 ) Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2010 56 88 87 91 83 82 90 68 2011 100 64 64 62 85 51 76 91 53 94 80 93 2012 77 73 53 59 88 71 98 89 74 66 91 57 2013 71 50 67 91 70 60 51 71 99 73 95 52 2014 57 72 82 72
总结:runif(48,min=50,max=100)表示随机生成均匀分布d48个数值,最小值为50,最大值为100。round表示四舍五入取整。ts可以将向量转换为时间序列,ts中的frequency值为1,表示以年为单位,如果值为4,表示以季度为单位,如果值为12,表示以月为单位,没有以天为单位的,一般时间序列不用天为单位。
2.11 常见错误
注意:变量赋值要用c,需要注意括号的使用,字符串需要加上引号。在R语言中文件地址用正斜线,反斜线用来转义。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 > x <- c ( 1 , 2 , 3 ) > x[ 1 ] 1 2 3 > x <- matrix( c ( 1 : 20 , seq( 1 , 12 , 3 ) , 4 , 4 ) ) > x [ , 1 ] [ 1 , ] 1 [ 2 , ] 2 [ 3 , ] 3 [ 4 , ] 4 [ 5 , ] 5 [ 6 , ] 6 [ 7 , ] 7 [ 8 , ] 8 [ 9 , ] 9 [ 10 , ] 10 [ 11 , ] 11 [ 12 , ] 12 [ 13 , ] 13 [ 14 , ] 14 [ 15 , ] 15 [ 16 , ] 16 [ 17 , ] 17 [ 18 , ] 18 [ 19 , ] 19 [ 20 , ] 20 [ 21 , ] 1 [ 22 , ] 4 [ 23 , ] 7 [ 24 , ] 10 [ 25 , ] 4 [ 26 , ] 4 > getwd( ) [ 1 ] "C:/Users/ywwsn/Documents" > setwd( "c:\\Users\\Default" ) > setwd( "c:/Users/Default" )
如果出现错误,可以访问网站进行解决,比如Google、Rblogger、quickR、stackoverflow等。
3 数据基本操作
3.1 获取数据
R获取数据三种途径:
利用键盘来输入数据;
通过读取存储在外部文件上的数据;
通过访问数据库系统来获取数据。
手动输入方式:
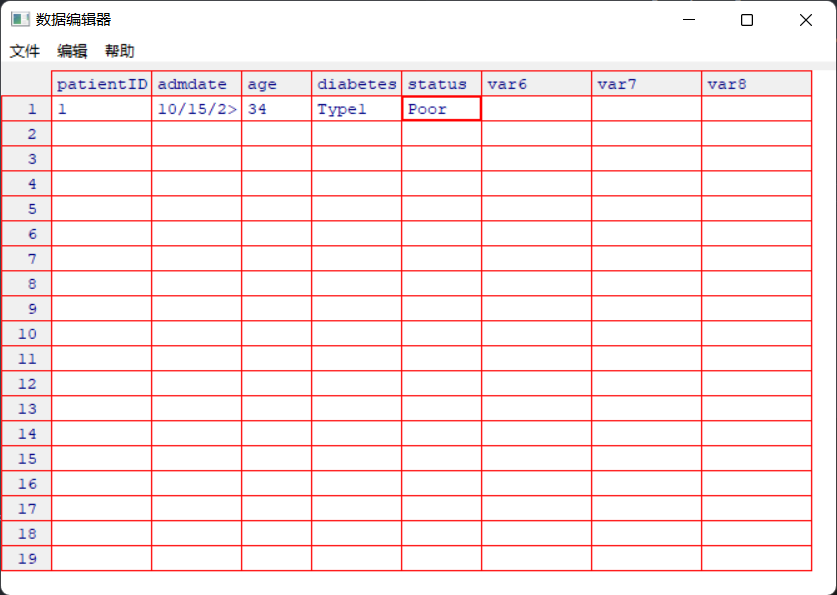
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > status <- c ( "Poor" , "Improved" , "Excellent" , "Poor" ) > data <- data.frame( patientID, age, diabetes, status) > data patientID age diabetes status 1 1 25 Type1 Poor2 2 34 Type2 Improved3 3 28 Type1 Excellent4 4 52 Type1 Poor> data2 <- data.frame( patientID= character( 0 ) , admdate= character( 0 ) , age= numeric( ) , diabetes= character( ) , status= character( ) ) > data2[ 1 ] patientID admdate age diabetes status < 0 行> ( 或0 - 长度的row.names) > data2 <- edit( data2) > data2 patientID admdate age diabetes status 1 1 10 / 15 / 200 25 Type1 Poor2 2 11 / 01 / 2009 34 Type2 Improved3 3 10 / 21 / 2009 28 Type1 Excellent4 4 10 / 28 / 2009 52 Type1 Poor
在运行data2 <- edit(data2)命令时会弹出下面的数据编辑器,进行数据输入:
在linux系统中如果无法打开数据编辑器,可以用vim进行编辑。
也可以使用fix函数启动数据编辑器进行边界,fix修改后会直接保存。
通过IDBC访问数据库,ODBC(Open Database Connectivity)是开放数据库连接。
在R中,可以RODBC包连接和访问数据库。:
1 > install.packages( "RODBC" )
RODBC包允许R和一个通过ODBC连接的SQL数据库之间进行双向的通信,这样不仅可以用R读取数据库的内容,同时还可以将R处理过的数据写入数据库中。需要使用MySQL、SQLlite包就下载相应的包。
3.2 读取文件
读取纯文本文件,可以使用read.table函数,将读取的文件赋值给一个参数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 > x <- read.table( "input.txt" ) > head( x) Ozone Solar.R Wind Temp Month Day 1 41 190 7.4 67 5 1 2 36 118 8.0 72 5 2 3 12 149 12.6 74 5 3 4 18 313 11.5 62 5 4 5 NA NA 14.3 56 5 5 6 28 NA 14.9 66 5 6 > tail( x) Ozone Solar.R Wind Temp Month Day 148 14 20 16.6 63 9 25 149 30 193 6.9 70 9 26 150 NA 145 13.2 77 9 27 151 14 191 14.3 75 9 28 152 18 131 8.0 76 9 29 153 20 223 11.5 68 9 30 x <- read.table( "f:/Learning/R语言入门与数据分析/RData/input.txt" ) > x <- read.table( "input.csv" ) > x V1 V2 1 , "mpg" , "cyl" , "disp" , "hp" , "drat" , "wt" , "qsec" , "vs" , "am" , "gear" , "carb" 2 Mazda RX4 , 21 , 6 , 160 , 110 , 3.9 , 2.62 , 16.46 , 0 , 1 , 4 , 4 3 Mazda RX4 Wag , 21 , 6 , 160 , 110 , 3.9 , 2.875 , 17.02 , 0 , 1 , 4 , 4 4 Datsun 710 , 22.8 , 4 , 108 , 93 , 3.85 , 2.32 , 18.61 , 1 , 1 , 4 , 1 ... 31 Ferrari Dino , 19.7 , 6 , 145 , 175 , 3.62 , 2.77 , 15.5 , 0 , 1 , 5 , 6 32 Maserati Bora , 15 , 8 , 301 , 335 , 3.54 , 3.57 , 14.6 , 0 , 1 , 5 , 8 33 Volvo 142 E , 21.4 , 4 , 121 , 109 , 4.11 , 2.78 , 18.6 , 1 , 1 , 4 , 2 > x <- read.table( "input.csv" , sep = "," ) > x V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 1 mpg cyl disp hp drat wt qsec vs am gear carb2 Mazda RX4 21 6 160 110 3.9 2.62 16.46 0 1 4 4 3 Mazda RX4 Wag 21 6 160 110 3.9 2.875 17.02 0 1 4 4 4 Datsun 710 22.8 4 108 93 3.85 2.32 18.61 1 1 4 1 ... 31 Ferrari Dino 19.7 6 145 175 3.62 2.77 15.5 0 1 5 6 32 Maserati Bora 15 8 301 335 3.54 3.57 14.6 0 1 5 8 33 Volvo 142 E 21.4 4 121 109 4.11 2.78 18.6 1 1 4 2 > x <- read.table( "input.csv" , sep = "," , header = TRUE ) > x X mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... 30 Ferrari Dino 19.7 6 145 175 3.62 2.77 15.5 0 1 5 6 31 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 32 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 > x <- read.table( "input 1.txt" , header = TRUE , skip = 5 ) > x Ozone Solar.R Wind Temp Month Day 1 41 190 7.4 67 5 1 2 36 118 8.0 72 5 2 3 12 149 12.6 74 5 3 ... 151 14 191 14.3 75 9 28 152 18 131 8.0 76 9 29 153 20 223 11.5 68 9 30 > x <- read.table( "input 1.txt" , header = TRUE , skip = 6 , nrows = 6 ) > x X1 X41 X190 X7.4 X67 X5 X1.1 1 2 36 118 8.0 72 5 2 2 3 12 149 12.6 74 5 3 3 4 18 313 11.5 62 5 4 4 5 NA NA 14.3 56 5 5 5 6 28 NA 14.9 66 5 6 6 7 23 299 8.6 65 5 7
总结:这里的head为显示x的头部6行,tail为显示x的尾部6行。read.table读取的文件可以写全局路径。如果读写的是csv文件,需要将分隔符设为,。否则会出现问题,如果想知道用什么分隔符,可以打开文件看看。header参数如果为TRUE表示将第一行作为变量名称。skip参数用来跳过部分内容,比如有些数据会有介绍性文字。通过skip和nrows组合可以读取任意一段数据。na.strings参数可以将设定的其他软件中的缺失符号替换为NA,NA属于R中的缺失值。stringAsFactors控制读入的字符串是否转换成因子,R读取数据时,数字被读取成数值型数据,而在读取字符串时,会默认将读取的字符串转为因子类型,但是很多情况下不需要这样的转换,因此需要将stringAsFactors设为FALSE。
除了read.table函数,还有read.csv函数,read.csv函数默认用,分隔。read.delim表示读取用制表符分割的文件,read.fwf表示读取固定宽度的文件,每一列都开始于固定的位置,例如:
1 read.fwf( "fwf.txt" , widths = c ( 2 , 3 , 4 ) )
使用read.fwf需要用widths参数给定每一列所占用的宽度值。这种文件使用的不多。
R还支持读取网络文件,read.table会将文件下载到本地。
1 x <- read.table( "https://codeload.github.com/mperdeck/LINQtoCSV/zip/master" , header = TRUE )
如果读取网页中的数据,需要安装包XML,然后通过readHTMLTable函数进行读取,如果想读取网页中第三个表格的数据,可以将which参数值设为3。
可以通过foreign包中的函数对其他软件格式的数据进行导入。
1 help(package = "foreign")
如果其他格式的文件不在foreign包中,一种方法就是另存为文本文件,另一种就是搜索R中对应的包,例如搜索能够读取Matlab相关格式的包,如下所示:
R还支持读取剪贴板的数据:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > x <- read.table( "clipboard" , header = T , sep = "\t" ) > x X mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 4 Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 5 Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 > readClipboard( ) [ 1 ] "\tmpg\tcyl\tdisp\thp\tdrat\twt\tqsec\tvs\tam\tgear\tcarb" [ 2 ] "Mazda RX4\t21\t6\t160\t110\t3.9\t2.62\t16.46\t0\t1\t4\t4" [ 3 ] "Mazda RX4 Wag\t21\t6\t160\t110\t3.9\t2.875\t17.02\t0\t1\t4\t4" [ 4 ] "Datsun 710\t22.8\t4\t108\t93\t3.85\t2.32\t18.61\t1\t1\t4\t1" [ 5 ] "Hornet 4 Drive\t21.4\t6\t258\t110\t3.08\t3.215\t19.44\t1\t0\t3\t1" [ 6 ] "Hornet Sportabout\t18.7\t8\t360\t175\t3.15\t3.44\t17.02\t0\t0\t3\t2"
总结:可以通过read.table("clipboard",header = T, sep = "\t")来读取剪贴板中的表格数据;或者通过readClipboard函数也可以直接读取。
R也可以直接读取压缩文件:
1 > read.table( gzfile( "input.txt.gz" ) )
如果遇到不标准的文件格式,可以通过readLines函数和scan函数来处理,根据每一行甚至每一单元来读取文件。readLines通过字符串的形式显示访问结果。
1 readLines( "input.csv" , n= 5 )
其中n表示读入的最大行数
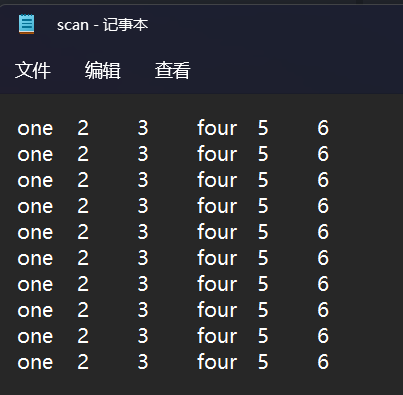
scan每读取一个单元,根据指令进行处理,第一个参数为文件的地址,用来描述scan所期望输入文件的单元,第二个参数为what,指定读写数据的类型,是数值型、整型还是逻辑型,scan函数可以重复执行指定的模式,直到读取所有需要的数据。
1 2 3 4 5 6 7 8 9 10 11 > scan( "scan.txt" , what = list ( X1 = character( 0 ) , X2 = numeric( 0 ) , X3 = numeric( 0 ) ) ) Read 20 records $ X1 [ 1 ] "one" "four" "one" "four" "one" "four" "one" "four" "one" "four" "one" "four" "one" "four" "one" "four" "one" [ 18 ] "four" "one" "four" $ X2 [ 1 ] 2 5 2 5 2 5 2 5 2 5 2 5 2 5 2 5 2 5 2 5 $ X3 [ 1 ] 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6
这里character表示首先读取3个字符串内容,然后再分别读取两次数值,因为给定的数据呈现一个规律:第一列先是一个字符,然后两列数字,后面第四列往后也是同样的规律。
3.3 写入文件
写入文件有两种方法,分别为write和cat,write是将数据写入文件中,而cat是将数据显示在屏幕上。
也可以将文件保存某个存在的目录中,因为R不能够创建不存在的目录。如果不设定目录,就会自动保存在当前目录中。
1 2 3 > write.table( x, file = "newfile.txt" ) > write.table( x, file = "f:/Learning/R语言入门与数据分析/RData/newnew.txt" ) > write.table( x, file = "f:/Learning/R语言入门与数据分析/RData/newnew.csv" , sep = "," )
写入的时候会自动添加行号,可以设定write.table函数中的参数row.names为FALSE,这样写入的文档就不会包含行号:
1 > write.table( x, file = "f:/Learning/R语言入门与数据分析/RData/newnew.txt" , sep = "," , row.names = FALSE )
写入文件为txt格式时,会默认会添加双引号,如果不需要,可以设定write.table函数中的参数quote为FALSE。
默认如果写入的是同名的文件,R会覆盖掉原来的文件,如果要将数据写入同一个文件,可以设定write.table函数中的参数append为TRUE,数据会写入文件的结尾;如果为FALSE会覆盖掉原来的文件,和R语言默认相同。
1 2 3 4 > write.table( iris, file = "f:/Learning/R语言入门与数据分析/RData/newnew.txt" , append = T ) Warning message: In write.table( iris, file = "f:/Learning/R语言入门与数据分析/RData/newnew.txt" , : 给文件加列名
虽然有警告,但是已经成功将数据追加到newnew.txt文件后面。
R也支持写入压缩文件:
1 write.table( mtcars, gzfile( "newfile.txt.gz" ) )
如果想将数据结果写为其他软件的数据格式,可以通过foreign包来学习保存什么格式:
1 help( package = "foreign" )
3.4 读Excel文件
如果涉及到xlsx文件格式,需要安装XLConnect包
读入Excel文件:
1 2 3 4 5 6 7 8 9 10 > x <- read.csv( "mtcars.csv" , header = TRUE ) > x X mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... 30 Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 31 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 32 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2
也可以复制表格中相应的内容,然后读取剪贴板内容:
1 2 3 4 5 6 7 8 > x <- read.csv( "clipboard" , sep = "\t" , header = TRUE ) > x X mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 4 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 5 Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
如果涉及到xlsx文件格式,需要加载XLConnect包
一步法 :通过readWorksheetFromFile函数进行操作。
1 2 3 4 5 6 7 8 9 > readWorksheetFromFile( "data.xlsx" , 1 ) Col1 mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 ... 30 Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 31 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 32 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2
其中数字1表示第几个工作簿。
两步法 :
1 2 3 4 5 6 7 8 9 10 > ex <- loadWorkbook( "data.xlsx" ) > edata <- readWorksheet( ex, 1 ) > head( edata) Col1 mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 3 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 4 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 5 Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 6 Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
loadWorkbook表示读取的是xlsx文件,通过readWorksheet函数读取ex的第1个工作表。
可以使用header函数查看是否有问题。
也可以通过readWorksheet函数指定工作表的范围,如下所示:
1 2 3 4 5 6 7 8 9 10 11 > readWorksheet( ex, 1 , startRow = 0 , startCol = 0 , endRow = 10 , endCol = 3 , header = TRUE ) Col1 mpg cyl 1 Mazda RX4 21.0 6 2 Mazda RX4 Wag 21.0 6 3 Datsun 710 22.8 4 4 Hornet 4 Drive 21.4 6 5 Hornet Sportabout 18.7 8 6 Valiant 18.1 6 7 Duster 360 14.3 8 8 Merc 240 D 24.4 4 9 Merc 230 22.8 4
header表示是否读取表头,如果为TRUE,表示读取表头。
3.5 写Excel文件
一步法 :通过writeWorksheetToFile函数即可完成。
1 > writeWorksheetToFile( "file.xlsx" , data = mtcars, sheet = "sheet 1" )
这里file.xlsx为写入的文件名,data为写入的数据,sheet为工作簿编号。data和sheet都支持列表的数据格式。
四步法 :
使用loadWorkbook创建一个工作表,即一个文件;
1 > wb = loadWorkbook( "file.xlsx" , create = T )
使用createSheet函数在工作表中创建工作簿;
1 > createSheet( wb, "Sheet 1" )
使用writeWorksheet函数将数据保存到工作簿中;
1 > writeWorksheet( wb, data= mtcars, sheet = "sheet 1" )
使用saveWorkbook函数将工作表存储为Excel文件。
更多内容可以查看这个包的帮助文档vignette,可以通过以下命令查看:
如果只是简单读写Excel文件,也可以用xlsl包。
1 2 install.packages( "xlsx" ) library( xlsx)
可以通过help(package=xlsx)进行查看相关使用方法。
示例:
1 2 > x <- read.xlsx( "data.xlsx" , 1 , startRow = 1 , endRow = 10 ) > write.xlsx( x, file = "rdata.xlsx" , sheetName = "Sheet 1" , append = F )
3.6 读写R格式文件
RDS文件可以存储单个R对象,而RData可以保存多个R对象。RDS文件和RData文件不能保存图形,只能单独保存图片。
存储为R文件有很多优势,R会对存储为内部文件格式的数据进行自动压缩处理,并且会存储所有与待存储对象相关的R元数据。如果数据中包含了因子,日期和时间或者类的属性等信息。
1 > saveRDS( iris, file = "iris.RDS" )
总结:saveRDS函数将数据保存为RDS文件。
1 > x <- readRDS( "iris.RDS" )
总结:readRDS是读取RDS文件的函数。
可以通过load函数载入RData文件,例如:
1 2 load( "ch03.R" ) load( ".RData" )
注意:如果需要载入的对象和当前R工作空间中的对象重名,会将当前工作空间中的对象数据进行覆盖。在加载文件之前需要对文件内容有所了解,如果打开新的文件,就不用担心这些问题了。
保存为RData文件直接使用save函数即可:
1 > save( iris, iris3, file = "newiris.Rdata" )
前几个是保存的对象名称,file为保存的文件地址。
如果想保存当前工作空间中所有对象,直接通过save.image函数即可。
4 数据转换
数据转换是对R进行数据操作的核心内容。
4.1 数据格式转换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 > library( xlsx) > cars32 <- read.xlsx( "mtcars.xlsx" , sheetIndex = 1 , header = T ) > cars32 NA. mpg cyl disp hp drat wt qsec vs am gear carb 1 Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 2 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 ... 30 Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 31 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 32 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 > is.data.frame( cars32) [ 1 ] TRUE > state.x77 Population Income Illiteracy Life Exp Murder HS Grad Frost Area Alabama 3615 3624 2.1 69.05 15.1 41.3 20 50708 Alaska 365 6315 1.5 69.31 11.3 66.7 152 566432 Arizona 2212 4530 1.8 70.55 7.8 58.1 15 113417 ... West Virginia 1799 3617 1.4 69.48 6.7 41.6 100 24070 Wisconsin 4589 4468 0.7 72.48 3.0 54.5 149 54464 Wyoming 376 4566 0.6 70.29 6.9 62.9 173 97203 > is.data.frame( state.x77) [ 1 ] FALSE > dstate.x77 <- as.data.frame( state.x77) > is.data.frame( dstate.x77) [ 1 ] TRUE
总结:is.data.frame函数可以判断对象是否为数据框,as.data.frame可以将对象强制转换成数据框的结构。上面的示例为矩阵转为数据框。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > data.frame( state.region, state.x77) state.region Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Alabama South 3615 3624 2.1 69.05 15.1 41.3 20 50708 Alaska West 365 6315 1.5 69.31 11.3 66.7 152 566432 Arizona West 2212 4530 1.8 70.55 7.8 58.1 15 113417 ... West Virginia South 1799 3617 1.4 69.48 6.7 41.6 100 24070 Wisconsin North Central 4589 4468 0.7 72.48 3.0 54.5 149 54464 Wyoming West 376 4566 0.6 70.29 6.9 62.9 173 97203 > as.matrix( data.frame( state.region, state.x77) ) state.region Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Alabama "South" " 3615" "3624" "2.1" "69.05" "15.1" "41.3" " 20" " 50708" Alaska "West" " 365" "6315" "1.5" "69.31" "11.3" "66.7" "152" "566432" Arizona "West" " 2212" "4530" "1.8" "70.55" " 7.8" "58.1" " 15" "113417" ... West Virginia "South" " 1799" "3617" "1.4" "69.48" " 6.7" "41.6" "100" " 24070" Wisconsin "North Central" " 4589" "4468" "0.7" "72.48" " 3.0" "54.5" "149" " 54464" Wyoming "West" " 376" "4566" "0.6" "70.29" " 6.9" "62.9" "173" " 97203"
总结:如果数据框中存在字符串,在将数据框转换成矩阵时,会将数值也转换成字符串进行处理。
注意:并不是所有的数据转换都起作用,有些无法进行转换。
更多示例可以通过methods函数查看示例:
R中最基础的就是向量,可以转换成多种数据格式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 > x <- state.abb> x [ 1 ] "AL" "AK" "AZ" "AR" "CA" "CO" "CT" "DE" "FL" "GA" "HI" "ID" "IL" "IN" "IA" "KS" "KY" "LA" "ME" "MD" "MA" "MI" "MN" "MS" [ 25 ] "MO" "MT" "NE" "NV" "NH" "NJ" "NM" "NY" "NC" "ND" "OH" "OK" "OR" "PA" "RI" "SC" "SD" "TN" "TX" "UT" "VT" "VA" "WA" "WV" [ 49 ] "WI" "WY" > dim ( x) <- c ( 5 , 10 ) > x [ , 1 ] [ , 2 ] [ , 3 ] [ , 4 ] [ , 5 ] [ , 6 ] [ , 7 ] [ , 8 ] [ , 9 ] [ , 10 ] [ 1 , ] "AL" "CO" "HI" "KS" "MA" "MT" "NM" "OK" "SD" "VA" [ 2 , ] "AK" "CT" "ID" "KY" "MI" "NE" "NY" "OR" "TN" "WA" [ 3 , ] "AZ" "DE" "IL" "LA" "MN" "NV" "NC" "PA" "TX" "WV" [ 4 , ] "AR" "FL" "IN" "ME" "MS" "NH" "ND" "RI" "UT" "WI" [ 5 , ] "CA" "GA" "IA" "MD" "MO" "NJ" "OH" "SC" "VT" "WY" > as.factor( x) [ 1 ] AL AK AZ AR CA CO CT DE FL GA HI ID IL IN IA KS KY LA ME MD MA MI MN MS MO MT NE NV NH NJ NM NY NC ND OH OK OR PA RI SC SD [ 42 ] TN TX UT VT VA WA WV WI WY50 Levels: AK AL AR AZ CA CO CT DE FL GA HI IA ID IL IN KS KY LA MA MD ME MI MN MO MS MT NC ND NE NH NJ NM NV NY OH OK ... WY> as.list( x) [[ 1 ] ] [ 1 ] "AL" [[ 2 ] ] [ 1 ] "AK" [[ 3 ] ] [ 1 ] "AZ" ... [[ 48 ] ] [ 1 ] "WV" [[ 49 ] ] [ 1 ] "WI" [[ 50 ] ] [ 1 ] "WY" > state <- data.frame( x, state.region, state.x77) > state$ Income [ 1 ] 3624 6315 4530 3378 5114 4884 5348 4809 4815 4091 4963 4119 5107 4458 4628 4669 3712 3545 3694 5299 4755 4751 4675 3098 [ 25 ] 4254 4347 4508 5149 4281 5237 3601 4903 3875 5087 4561 3983 4660 4449 4558 3635 4167 3821 4188 4022 3907 4701 4864 3617 [ 49 ] 4468 4566 > state[ "Nevada" , ] X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 state.region Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Nevada AZ DE IL LA MN NV NC PA TX WV West 590 5149 0.5 69.03 11.5 65.2 188 109889 > is.data.frame( state[ "Nevada" , ] ) [ 1 ] TRUE > y <- state[ "Nevada" , ] > y X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 state.region Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Nevada AZ DE IL LA MN NV NC PA TX WV West 590 5149 0.5 69.03 11.5 65.2 188 109889 > unname( y) Nevada AZ DE IL LA MN NV NC PA TX WV West 590 5149 0.5 69.03 11.5 65.2 188 109889 > unlist( y) X1 X2 X3 X4 X5 X6 X7 X8 X9 "AZ" "DE" "IL" "LA" "MN" "NV" "NC" "PA" "TX" X10 state.region Population Income Illiteracy Life.Exp Murder HS.Grad Frost "WV" "4" "590" "5149" "0.5" "69.03" "11.5" "65.2" "188" Area "109889"
数据框取出列可以用$符号,取出行用state["Nevada",],注意不要忘记逗号。如果想去除列名,可以通过unname函数。如果想将其转换成向量,可以使用unlist函数。
4.2 数据部分提取
1 2 3 4 5 > who <- read.csv( "WHO.csv" , header = T ) > who1 <- who[ c ( 1 : 50 ) , c ( 1 : 10 ) ] > who2 <- who[ c ( 1 , 3 , 5 , 8 ) , c ( 2 , 14 , 16 , 18 ) ] > who3 <- who[ which( who$ Continent== 7 ) , ] > who4 <- who[ which( who$ CountryID> 50 & who$ CountryID<= 100 ) ]
总结:可以提取连续的部分内容,如who1;也可以提取零散的部分内容,如who2;也可以根据逻辑值进行提取,如who3;也可以取某个范围的值,如who4。
取子集也可以用subset函数。
1 > who4 <- subset( who, who$ CountryID> 50 & who$ CountryID<= 100 )
在数学挖掘和机器学习领域,从更大的数据集中抽样是常见的做法,例如随机抽取两个样本,一个样本用来建模,另一类样本用来验证有效性。R中可以用sample函数用来随机抽样。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > x <- 1: 100 > x [ 1 ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [ 28 ] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 [ 55 ] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 [ 82 ] 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 > sample( x, 60 ) [ 1 ] 97 8 5 33 88 28 48 34 39 69 35 82 81 50 92 12 16 87 17 76 98 40 74 75 19 54 11 [ 28 ] 49 30 32 89 70 37 13 96 72 25 1 78 14 60 57 58 23 95 90 15 83 52 100 64 38 86 51 [ 55 ] 45 3 99 2 93 27 > sample( x, 60 , replace = T ) [ 1 ] 41 57 24 1 67 25 41 64 23 6 65 72 65 68 29 37 78 72 26 55 86 25 2 69 93 58 68 [ 28 ] 92 26 69 64 72 54 77 65 75 25 45 68 53 60 20 95 94 28 18 99 22 8 90 82 14 95 32 [ 55 ] 42 88 76 78 100 25 > sort( sample( x, 60 , replace = T ) ) [ 1 ] 4 8 8 9 9 14 14 17 19 21 26 26 27 27 28 29 30 30 32 34 34 39 41 44 50 50 51 53 56 56 57 58 59 59 60 64 [ 37 ] 66 67 68 71 71 72 72 75 75 76 76 81 85 86 87 88 90 90 92 93 93 96 96 98 > who <- read.csv( "WHO.csv" , header = T ) > who[ sample( who$ CountryID, 30 , replace = F ) , ]
总结:sample抽样默认是无返回抽样,如果sample函数中replace逻辑值设为T,则为有放回抽样。
删除固定行,最简单的方式就是负索引的方式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 > mtcars mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 > mtcars[ - 1 : - 5 , ] mpg cyl disp hp drat wt qsec vs am gear carb Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 > mtcars[ , - 1 : - 5 ] wt qsec vs am gear carb Mazda RX4 2.620 16.46 0 1 4 4 Mazda RX4 Wag 2.875 17.02 0 1 4 4 Datsun 710 2.320 18.61 1 1 4 1 Hornet 4 Drive 3.215 19.44 1 0 3 1 Hornet Sportabout 3.440 17.02 0 0 3 2 Valiant 3.460 20.22 1 0 3 1 Duster 360 3.570 15.84 0 0 3 4 Merc 240 D 3.190 20.00 1 0 4 2 ... Ferrari Dino 2.770 15.50 0 1 5 6 Maserati Bora 3.570 14.60 0 1 5 8 Volvo 142 E 2.780 18.60 1 1 4 2
总结:可以通过负索引的方式进行删除相应的行或列。
1 2 3 4 5 6 7 8 9 > mtcars$ mpg <- NULL > head( mtcars) cyl disp hp drat wt qsec vs am gear carb Mazda RX4 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 6 160 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 4 108 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 8 360 175 3.15 3.440 17.02 0 0 3 2 Valiant 6 225 105 2.76 3.460 20.22 1 0 3 1
总结:也可以通过置空来进行删除相应的列,例如mtcars$mpg <-NULL。注意NULL要大写。
4.3 数据合并与去重
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 > USArrests Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 ... West Virginia 5.7 81 39 9.3 Wisconsin 2.6 53 66 10.8 Wyoming 6.8 161 60 15.6 > state.division [ 1 ] East South Central Pacific Mountain West South Central Pacific [ 6 ] Mountain New England South Atlantic South Atlantic South Atlantic [ 11 ] Pacific Mountain East North Central East North Central West North Central[ 16 ] West North Central East South Central West South Central New England South Atlantic [ 21 ] New England East North Central West North Central East South Central West North Central[ 26 ] Mountain West North Central Mountain New England Middle Atlantic [ 31 ] Mountain Middle Atlantic South Atlantic West North Central East North Central[ 36 ] West South Central Pacific Middle Atlantic New England South Atlantic [ 41 ] West North Central East South Central West South Central Mountain New England [ 46 ] South Atlantic Pacific South Atlantic East North Central Mountain 9 Levels: New England Middle Atlantic South Atlantic East South Central ... Pacific> data.frame( USArrests, state.division) Murder Assault UrbanPop Rape state.division Alabama 13.2 236 58 21.2 East South Central Alaska 10.0 263 48 44.5 Pacific Arizona 8.1 294 80 31.0 Mountain ... West Virginia 5.7 81 39 9.3 South Atlantic Wisconsin 2.6 53 66 10.8 East North Central Wyoming 6.8 161 60 15.6 Mountain
总结:data.frame函数可以来合并两个对象为数据框。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > cbind( USArrests, state.division) Murder Assault UrbanPop Rape state.division Alabama 13.2 236 58 21.2 East South Central Alaska 10.0 263 48 44.5 Pacific Arizona 8.1 294 80 31.0 Mountain ... West Virginia 5.7 81 39 9.3 South Atlantic Wisconsin 2.6 53 66 10.8 East North Central Wyoming 6.8 161 60 15.6 Mountain > data1 <- head( USArrests, 2 ) > data1 Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 > data2 <- tail( USArrests, 2 ) > data2 Murder Assault UrbanPop Rape Wisconsin 2.6 53 66 10.8 Wyoming 6.8 161 60 15.6 > rbind( data1, data2) Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Wisconsin 2.6 53 66 10.8 Wyoming 6.8 161 60 15.6
总结:可以通过cbind和rbind函数进行列合并和行合并,合并列很容易,合并行需要有相同的列名。cbind和rbind也可以用于矩阵合并。在使用cbind和rbind中需要有相同的行数和列数,否则会出现问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 > datadata1 <- USArrests[ 1 : 5 , ] > datadata1 Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 > datadata2 <- USArrests[ 3 : 8 , ] > datadata2 Murder Assault UrbanPop Rape Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Colorado 7.9 204 78 38.7 Connecticut 3.3 110 77 11.1 Delaware 5.9 238 72 15.8 > datadata3 <- rbind( datadata1, datadata2) > datadata3 Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Arizona1 8.1 294 80 31.0 Arkansas1 8.8 190 50 19.5 California1 9.0 276 91 40.6 Colorado 7.9 204 78 38.7 Connecticut 3.3 110 77 11.1 Delaware 5.9 238 72 15.8 > duplicated( datadata3) [ 1 ] FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE FALSE FALSE FALSE > datadata3[ duplicated( datadata3) , ] Murder Assault UrbanPop Rape Arizona1 8.1 294 80 31.0 Arkansas1 8.8 190 50 19.5 California1 9.0 276 91 40.6 > datadata3[ ! duplicated( datadata3) , ] Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Colorado 7.9 204 78 38.7 Connecticut 3.3 110 77 11.1 Delaware 5.9 238 72 15.8 > length ( rownames( datadata3[ ! duplicated( datadata3) , ] ) ) [ 1 ] 8
总结:rbind合并并不会去除重复,可以通过行名来判断是否重复。可以通过duplicated来判断是否重复,还可以通过datadata3[duplicated(datadata3),]来提取重复的部分,且重复的行名后面自动添加了1。如果加上取反符号!则取出非重复的部分。这里使用逻辑值对函数进行索引。
1 2 3 4 5 6 7 8 9 10 > unique( datadata3) Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Colorado 7.9 204 78 38.7 Connecticut 3.3 110 77 11.1 Delaware 5.9 238 72 15.8
总结:也可以用unique函数直接去除重复的行。
4.4 数据翻转
翻转操作:将所有的行和列进行翻转
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > newdata <- USArrests[ 1 : 5 , ] > newdata Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 > scractm_newdata <- t( newdata) > scractm_newdata Alabama Alaska Arizona Arkansas California Murder 13.2 10.0 8.1 8.8 9.0 Assault 236.0 263.0 294.0 190.0 276.0 UrbanPop 58.0 48.0 80.0 50.0 91.0 Rape 21.2 44.5 31.0 19.5 40.6
单独进行某一行或者列进行反向,即进行前后顺序调换
1 2 3 4 > letters [ 1 ] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z" > rev( letters ) [ 1 ] "z" "y" "x" "w" "v" "u" "t" "s" "r" "q" "p" "o" "n" "m" "l" "k" "j" "i" "h" "g" "f" "e" "d" "c" "b" "a"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > women height weight 1 58 115 2 59 117 3 60 120 ... 13 70 154 14 71 159 15 72 164 > rownames( women) [ 1 ] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14" "15" > rev( rownames( women) ) [ 1 ] "15" "14" "13" "12" "11" "10" "9" "8" "7" "6" "5" "4" "3" "2" "1" > women[ rev( rownames( women) ) , ] height weight 15 72 164 14 71 159 13 70 154 ... 3 60 120 2 59 117 1 58 115
总结:可以通过rev函数进行前后顺序翻转。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 > data.frame( women$ height* 2.54 , women$ weight) women.height...2.54 women.weight 1 147.32 115 2 149.86 117 3 152.40 120 ... 13 177.80 154 14 180.34 159 15 182.88 164 > data.frame( height = women$ height* 2.54 , weight = women$ weight) height weight 1 147.32 115 2 149.86 117 3 152.40 120 ... 13 177.80 154 14 180.34 159 15 182.88 164 > transform( women, height= height* 2.54 ) height weight 1 147.32 115 2 149.86 117 3 152.40 120 ... 13 177.80 154 14 180.34 159 15 182.88 164 > transform( women, cm= height* 2.54 ) height weight cm 1 58 115 147.32 2 59 117 149.86 3 60 120 152.40 ... 13 70 154 177.80 14 71 159 180.34 15 72 164 182.88
总结:如果想修改某一行或者某一列的数据,可以通过data.frame进行重新组合,也可以采用更高效的方法,通过transform函数进行修改,也可以新增加一列。
4.5 数据排序
数据排序有三种函数:sort、order、rank
sort是对向量进行排序,返回值是排序后的结果向量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > rivers [ 1 ] 735 320 325 392 524 450 1459 135 465 600 330 336 280 315 870 906 202 329 290 1000 600 [ 22 ] 505 1450 840 1243 890 350 407 286 280 525 720 390 250 327 230 265 850 210 630 260 230 [ 43 ] 360 730 600 306 390 420 291 710 340 217 281 352 259 250 470 680 570 350 300 560 900 [ 64 ] 625 332 2348 1171 3710 2315 2533 780 280 410 460 260 255 431 350 760 618 338 981 1306 500 [ 85 ] 696 605 250 411 1054 735 233 435 490 310 460 383 375 1270 545 445 1885 380 300 380 377 [ 106 ] 425 276 210 800 420 350 360 538 1100 1205 314 237 610 360 540 1038 424 310 300 444 301 [ 127 ] 268 620 215 652 900 525 246 360 529 500 720 270 430 671 1770 > sort( rivers) [ 1 ] 135 202 210 210 215 217 230 230 233 237 246 250 250 250 255 259 260 260 265 268 270 [ 22 ] 276 280 280 280 281 286 290 291 300 300 300 301 306 310 310 314 315 320 325 327 329 [ 43 ] 330 332 336 338 340 350 350 350 350 352 360 360 360 360 375 377 380 380 383 390 390 [ 64 ] 392 407 410 411 420 420 424 425 430 431 435 444 445 450 460 460 465 470 490 500 500 [ 85 ] 505 524 525 525 529 538 540 545 560 570 600 600 600 605 610 618 620 625 630 652 671 [ 106 ] 680 696 710 720 720 730 735 735 760 780 800 840 850 870 890 900 900 906 981 1000 1038 [ 127 ] 1054 1100 1171 1205 1243 1270 1306 1450 1459 1770 1885 2315 2348 2533 3710 > rev( sort( rivers) ) [ 1 ] 3710 2533 2348 2315 1885 1770 1459 1450 1306 1270 1243 1205 1171 1100 1054 1038 1000 981 906 900 900 [ 22 ] 890 870 850 840 800 780 760 735 735 730 720 720 710 696 680 671 652 630 625 620 618 [ 43 ] 610 605 600 600 600 570 560 545 540 538 529 525 525 524 505 500 500 490 470 465 460 [ 64 ] 460 450 445 444 435 431 430 425 424 420 420 411 410 407 392 390 390 383 380 380 377 [ 85 ] 375 360 360 360 360 352 350 350 350 350 340 338 336 332 330 329 327 325 320 315 314 [ 106 ] 310 310 306 301 300 300 300 291 290 286 281 280 280 280 276 270 268 265 260 260 259 [ 127 ] 255 250 250 250 246 237 233 230 230 217 215 210 210 202 135 > sort( state.name) [ 1 ] "Alabama" "Alaska" "Arizona" "Arkansas" "California" "Colorado" [ 7 ] "Connecticut" "Delaware" "Florida" "Georgia" "Hawaii" "Idaho" [ 13 ] "Illinois" "Indiana" "Iowa" "Kansas" "Kentucky" "Louisiana" [ 19 ] "Maine" "Maryland" "Massachusetts" "Michigan" "Minnesota" "Mississippi" [ 25 ] "Missouri" "Montana" "Nebraska" "Nevada" "New Hampshire" "New Jersey" [ 31 ] "New Mexico" "New York" "North Carolina" "North Dakota" "Ohio" "Oklahoma" [ 37 ] "Oregon" "Pennsylvania" "Rhode Island" "South Carolina" "South Dakota" "Tennessee" [ 43 ] "Texas" "Utah" "Vermont" "Virginia" "Washington" "West Virginia" [ 49 ] "Wisconsin" "Wyoming"
总结:sort默认从小到大排列。字符串是按照ASCII码值顺序。如果需要从大到小排序,可以通过rev函数组合使用。sort只能用于向量,不能用于数据框的排序。
1 2 3 4 5 6 7 8 9 > mtcars[ sort( rownames( mtcars) ) , ] cyl disp hp drat wt qsec vs am gear carb AMC Javelin 8 304.0 150 3.15 3.435 17.30 0 0 3 2 Cadillac Fleetwood 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Camaro Z28 8 350.0 245 3.73 3.840 15.41 0 0 3 4 ... Toyota Corona 4 120.1 97 3.70 2.465 20.01 1 0 3 1 Valiant 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Volvo 142 E 4 121.0 109 4.11 2.780 18.60 1 1 4 2
总结:可以根据行的名称进行排序。
order排序:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 > sort( rivers) [ 1 ] 135 202 210 210 215 217 230 230 233 237 246 250 250 250 255 259 260 260 265 268 270 [ 22 ] 276 280 280 280 281 286 290 291 300 300 300 301 306 310 310 314 315 320 325 327 329 [ 43 ] 330 332 336 338 340 350 350 350 350 352 360 360 360 360 375 377 380 380 383 390 390 [ 64 ] 392 407 410 411 420 420 424 425 430 431 435 444 445 450 460 460 465 470 490 500 500 [ 85 ] 505 524 525 525 529 538 540 545 560 570 600 600 600 605 610 618 620 625 630 652 671 [ 106 ] 680 696 710 720 720 730 735 735 760 780 800 840 850 870 890 900 900 906 981 1000 1038 [ 127 ] 1054 1100 1171 1205 1243 1270 1306 1450 1459 1770 1885 2315 2348 2533 3710 > rivers [ 1 ] 735 320 325 392 524 450 1459 135 465 600 330 336 280 315 870 906 202 329 290 1000 600 [ 22 ] 505 1450 840 1243 890 350 407 286 280 525 720 390 250 327 230 265 850 210 630 260 230 [ 43 ] 360 730 600 306 390 420 291 710 340 217 281 352 259 250 470 680 570 350 300 560 900 [ 64 ] 625 332 2348 1171 3710 2315 2533 780 280 410 460 260 255 431 350 760 618 338 981 1306 500 [ 85 ] 696 605 250 411 1054 735 233 435 490 310 460 383 375 1270 545 445 1885 380 300 380 377 [ 106 ] 425 276 210 800 420 350 360 538 1100 1205 314 237 610 360 540 1038 424 310 300 444 301 [ 127 ] 268 620 215 652 900 525 246 360 529 500 720 270 430 671 1770 > order( rivers) [ 1 ] 8 17 39 108 129 52 36 42 91 117 133 34 56 87 76 55 41 75 37 127 138 107 13 30 72 53 29 [ 28 ] 19 49 61 103 124 126 46 94 123 116 14 2 3 35 18 11 65 12 81 51 27 60 78 111 54 43 112 [ 55 ] 119 134 97 105 102 104 96 33 47 4 28 73 88 48 110 122 106 139 77 92 125 100 6 74 95 9 57 [ 82 ] 93 84 136 22 5 31 132 135 113 120 99 62 59 10 21 45 86 118 80 128 64 40 130 140 58 85 50 [ 109 ] 32 137 44 1 90 79 71 109 24 38 15 26 63 131 16 82 20 121 89 114 67 115 25 98 83 23 7 [ 136 ] 141 101 69 66 70 68 > mtcars[ order( mtcars$ mpg) , ] mpg cyl disp hp drat wt qsec vs am gear carb Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 ... Fiat X1- 9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1 > mtcars[ order( - mtcars$ mpg) , ] mpg cyl disp hp drat wt qsec vs am gear carb Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2 Fiat X1- 9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1 ... Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4 Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4
总结:order也可以进行排序,返回的值是排序的位置,而不是排序后的结果。如果使order排序从大到小,需要在order参数中添加-号。
1 2 3 4 5 6 7 8 9 10 11 12 13 > mtcars[ order( mtcars$ mpg, mtcars$ disp) , ] mpg cyl disp hp drat wt qsec vs am gear carb Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 ... Fiat X1- 9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1
总结:也可以通过多个条件进行排序,比如在mpg相同时,disp越小的排在前面。
rank和sort、order不同,它是求秩的函数,它的返回值是这个向量对应元素的排名,具体操作不做介绍,可以通过?rank查看帮助文档。
4.6 数据统计
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 > WorldPhones N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer 1951 45939 21574 2876 1815 1646 89 555 1956 60423 29990 4708 2568 2366 1411 733 1957 64721 32510 5230 2695 2526 1546 773 1958 68484 35218 6662 2845 2691 1663 836 1959 71799 37598 6856 3000 2868 1769 911 1960 76036 40341 8220 3145 3054 1905 1008 1961 79831 43173 9053 3338 3224 2005 1076 > worldphone <- as.data.frame( WorldPhones) > worldphone N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer 1951 45939 21574 2876 1815 1646 89 555 1956 60423 29990 4708 2568 2366 1411 733 1957 64721 32510 5230 2695 2526 1546 773 1958 68484 35218 6662 2845 2691 1663 836 1959 71799 37598 6856 3000 2868 1769 911 1960 76036 40341 8220 3145 3054 1905 1008 1961 79831 43173 9053 3338 3224 2005 1076 > rs <- rowSums( worldphone) > rs 1951 1956 1957 1958 1959 1960 1961 74494 102199 110001 118399 124801 133709 141700 > cm <- colMeans( worldphone) > cm N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer 66747.5714 34343.4286 6229.2857 2772.2857 2625.0000 1484.0000 841.7143 > total <- cbind( worldphone, Total= rs) > total N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer Total 1951 45939 21574 2876 1815 1646 89 555 74494 1956 60423 29990 4708 2568 2366 1411 733 102199 1957 64721 32510 5230 2695 2526 1546 773 110001 1958 68484 35218 6662 2845 2691 1663 836 118399 1959 71799 37598 6856 3000 2868 1769 911 124801 1960 76036 40341 8220 3145 3054 1905 1008 133709 1961 79831 43173 9053 3338 3224 2005 1076 141700 > rbind( total, Mean = cm) N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer Total 1951 45939.00 21574.00 2876.000 1815.000 1646 89 555.0000 74494.00 1956 60423.00 29990.00 4708.000 2568.000 2366 1411 733.0000 102199.00 1957 64721.00 32510.00 5230.000 2695.000 2526 1546 773.0000 110001.00 1958 68484.00 35218.00 6662.000 2845.000 2691 1663 836.0000 118399.00 1959 71799.00 37598.00 6856.000 3000.000 2868 1769 911.0000 124801.00 1960 76036.00 40341.00 8220.000 3145.000 3054 1905 1008.0000 133709.00 1961 79831.00 43173.00 9053.000 3338.000 3224 2005 1076.0000 141700.00 Mean 66747.57 34343.43 6229.286 2772.286 2625 1484 841.7143 66747.57 Warning message: In rbind( deparse.level, ...) : number of columns of result, 8 , is not a multiple of vector length 7 of arg 2
也可以通过如下方式计算:
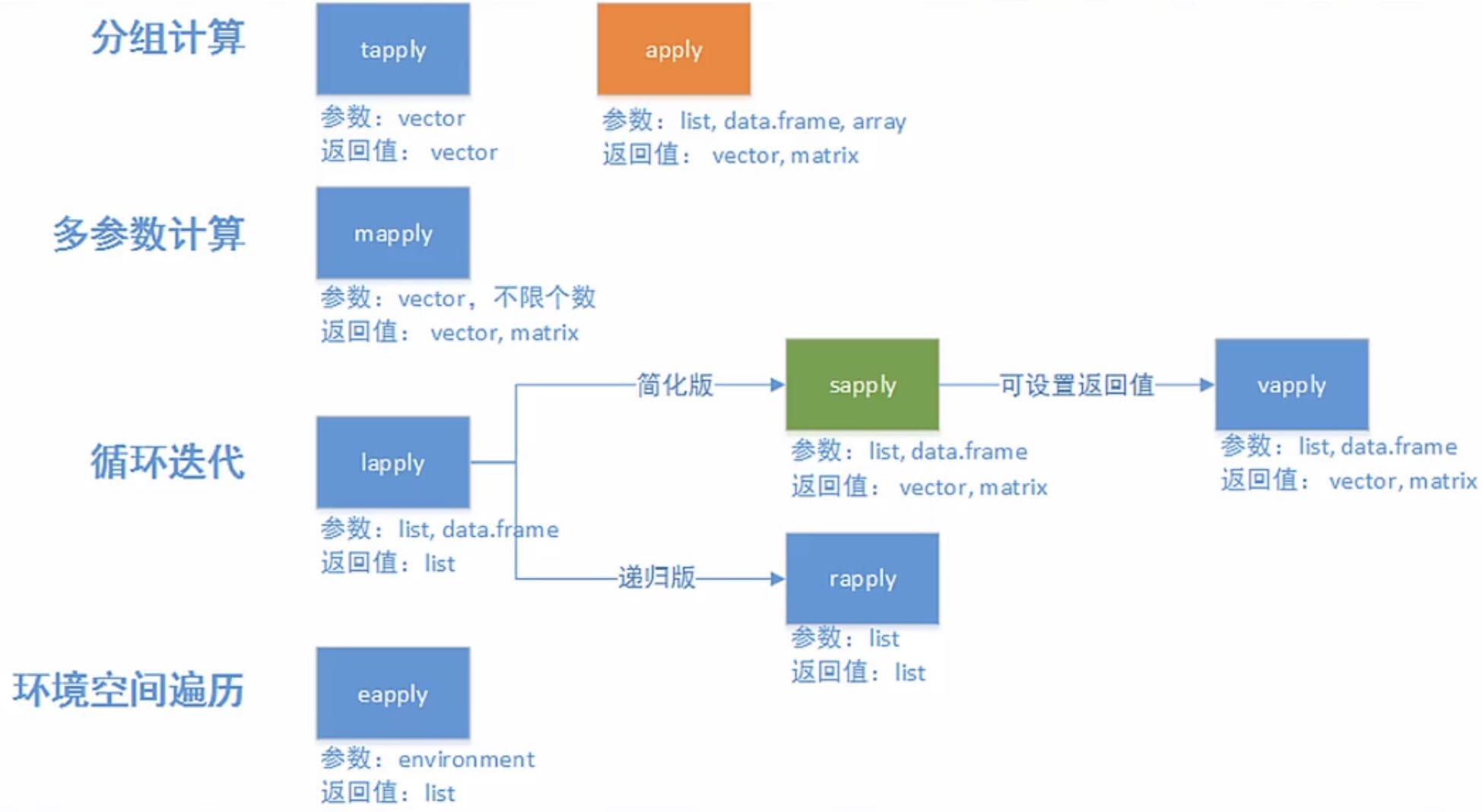
1 2 3 4 5 6 > apply( WorldPhones, MARGIN = 1 , FUN= sum ) 1951 1956 1957 1958 1959 1960 1961 74494 102199 110001 118399 124801 133709 141700 > apply( WorldPhones, MARGIN = 2 , FUN= mean) N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer 66747.5714 34343.4286 6229.2857 2772.2857 2625.0000 1484.0000 841.7143
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > state.center$ x [ 1 ] - 86.7509 - 127.2500 - 111.6250 - 92.2992 - 119.7730 - 105.5130 - 72.3573 - 74.9841 - 81.6850 - 83.3736 [ 11 ] - 126.2500 - 113.9300 - 89.3776 - 86.0808 - 93.3714 - 98.1156 - 84.7674 - 92.2724 - 68.9801 - 76.6459 [ 21 ] - 71.5800 - 84.6870 - 94.6043 - 89.8065 - 92.5137 - 109.3200 - 99.5898 - 116.8510 - 71.3924 - 74.2336 [ 31 ] - 105.9420 - 75.1449 - 78.4686 - 100.0990 - 82.5963 - 97.1239 - 120.0680 - 77.4500 - 71.1244 - 80.5056 [ 41 ] - 99.7238 - 86.4560 - 98.7857 - 111.3300 - 72.5450 - 78.2005 - 119.7460 - 80.6665 - 89.9941 - 107.2560 $ y [ 1 ] 32.5901 49.2500 34.2192 34.7336 36.5341 38.6777 41.5928 38.6777 27.8744 32.3329 31.7500 43.5648 40.0495 [ 14 ] 40.0495 41.9358 38.4204 37.3915 30.6181 45.6226 39.2778 42.3645 43.1361 46.3943 32.6758 38.3347 46.8230 [ 27 ] 41.3356 39.1063 43.3934 39.9637 34.4764 43.1361 35.4195 47.2517 40.2210 35.5053 43.9078 40.9069 41.5928 [ 40 ] 33.6190 44.3365 35.6767 31.3897 39.1063 44.2508 37.5630 47.4231 38.4204 44.5937 43.0504 > lapply( state.center, FUN= length ) $ x[ 1 ] 50 $ y[ 1 ] 50 > class ( lapply( state.center, FUN= length ) ) [ 1 ] "list" > class ( sapply( state.center, FUN= length ) ) [ 1 ] "integer"
下面是通过tapply统计每个区有几个州:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 > state.name [ 1 ] "Alabama" "Alaska" "Arizona" "Arkansas" "California" "Colorado" [ 7 ] "Connecticut" "Delaware" "Florida" "Georgia" "Hawaii" "Idaho" [ 13 ] "Illinois" "Indiana" "Iowa" "Kansas" "Kentucky" "Louisiana" [ 19 ] "Maine" "Maryland" "Massachusetts" "Michigan" "Minnesota" "Mississippi" [ 25 ] "Missouri" "Montana" "Nebraska" "Nevada" "New Hampshire" "New Jersey" [ 31 ] "New Mexico" "New York" "North Carolina" "North Dakota" "Ohio" "Oklahoma" [ 37 ] "Oregon" "Pennsylvania" "Rhode Island" "South Carolina" "South Dakota" "Tennessee" [ 43 ] "Texas" "Utah" "Vermont" "Virginia" "Washington" "West Virginia" [ 49 ] "Wisconsin" "Wyoming" > state.division [ 1 ] East South Central Pacific Mountain West South Central Pacific [ 6 ] Mountain New England South Atlantic South Atlantic South Atlantic [ 11 ] Pacific Mountain East North Central East North Central West North Central[ 16 ] West North Central East South Central West South Central New England South Atlantic [ 21 ] New England East North Central West North Central East South Central West North Central[ 26 ] Mountain West North Central Mountain New England Middle Atlantic [ 31 ] Mountain Middle Atlantic South Atlantic West North Central East North Central[ 36 ] West South Central Pacific Middle Atlantic New England South Atlantic [ 41 ] West North Central East South Central West South Central Mountain New England [ 46 ] South Atlantic Pacific South Atlantic East North Central Mountain 9 Levels: New England Middle Atlantic South Atlantic East South Central ... Pacific> tapply( state.name, state.division, FUN= length ) New England Middle Atlantic South Atlantic East South Central West South Central 6 3 8 4 4 East North Central West North Central Mountain Pacific 5 7 8 5
总结:
apply适用于数据框或矩阵。
lapply和sapply返回值的形式不同,lapply返回的是列表的形式,sapply返回的是向量或矩阵,比列表简单。列表没有行和列之分,不需要边界MARGIN参数。FUN函数可以是自带的函数,也可以是自定义函数。
tapply是用来处理因子数据,根据因子来分组,然后对每组分别处理。和apply类似,第一个参数为数据集,第二个必须为因子数据类型,通过因子对第一个参数进行分组,第三个参数FUN为要使用的函数。
还有相关函数的用法:
4.7 数据的中心化与标准化
数据中心化:是指数据集中的各项数据减去数据集的均值。
数据标准化:是指在中心化之后再除以数据集的标准差,即数据集中的各项数据减去数据集的均值再除以数据集的标准差。
标准差计算用sd函数,例如某个向量标准化处理后如下:
1 2 3 4 5 6 7 > x <- c ( 1 , 2 , 3 , 6 , 3 ) > mean( x) [ 1 ] 3 > sd( x) [ 1 ] 1.870829 > ( x- mean( x) ) / sd( x) [ 1 ] - 1.0690450 - 0.5345225 0.0000000 1.6035675 0.0000000
可以看出,标准化处理后的值之间相差变小。
R实现中心化和标准化可以使用scale函数:scale(x, center = TRUE, scale = TRUE)。如果center为TRUE,则为中心化处理,如果scale为TRUE,则为标准化处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 > head( state.x77) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Alabama 3615 3624 2.1 69.05 15.1 41.3 20 50708 Alaska 365 6315 1.5 69.31 11.3 66.7 152 566432 Arizona 2212 4530 1.8 70.55 7.8 58.1 15 113417 Arkansas 2110 3378 1.9 70.66 10.1 39.9 65 51945 California 21198 5114 1.1 71.71 10.3 62.6 20 156361 Colorado 2541 4884 0.7 72.06 6.8 63.9 166 103766 > xcenter <- scale( state.x77, center = T ) > head( xcenter) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Alabama - 0.1414316 - 1.3211387 1.525758 - 1.3621937 2.0918101 - 1.4619293 - 1.6248292 - 0.2347183 Alaska - 0.8693980 3.0582456 0.541398 - 1.1685098 1.0624293 1.6828035 0.9145676 5.8093497 Arizona - 0.4556891 0.1533029 1.033578 - 0.2447866 0.1143154 0.6180514 - 1.7210185 0.5002047 Arkansas - 0.4785360 - 1.7214837 1.197638 - 0.1628435 0.7373617 - 1.6352611 - 0.7591257 - 0.2202212 California 3.7969790 1.1037155 - 0.114842 0.6193415 0.7915396 1.1751891 - 1.6248292 1.0034903 Colorado - 0.3819965 0.7294092 - 0.771082 0.8800698 - 0.1565742 1.3361400 1.1838976 0.3870991 > xcenter <- scale( state.x77, center = T , scale = F ) > head( xcenter) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Alabama - 631.42 - 811.8 0.93 - 1.8286 7.722 - 11.808 - 84.46 - 20027.88 Alaska - 3881.42 1879.2 0.33 - 1.5686 3.922 13.592 47.54 495696.12 Arizona - 2034.42 94.2 0.63 - 0.3286 0.422 4.992 - 89.46 42681.12 Arkansas - 2136.42 - 1057.8 0.73 - 0.2186 2.722 - 13.208 - 39.46 - 18790.88 California 16951.58 678.2 - 0.07 0.8314 2.922 9.492 - 84.46 85625.12 Colorado - 1705.42 448.2 - 0.47 1.1814 - 0.578 10.792 61.54 33030.12 > xcale <- scale( state.x77, center = T , scale = T ) > head( xcale) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Alabama - 0.1414316 - 1.3211387 1.525758 - 1.3621937 2.0918101 - 1.4619293 - 1.6248292 - 0.2347183 Alaska - 0.8693980 3.0582456 0.541398 - 1.1685098 1.0624293 1.6828035 0.9145676 5.8093497 Arizona - 0.4556891 0.1533029 1.033578 - 0.2447866 0.1143154 0.6180514 - 1.7210185 0.5002047 Arkansas - 0.4785360 - 1.7214837 1.197638 - 0.1628435 0.7373617 - 1.6352611 - 0.7591257 - 0.2202212 California 3.7969790 1.1037155 - 0.114842 0.6193415 0.7915396 1.1751891 - 1.6248292 1.0034903 Colorado - 0.3819965 0.7294092 - 0.771082 0.8800698 - 0.1565742 1.3361400 1.1838976 0.3870991 > heatmap( xcale)
总结:可以通过标准化处理后,就能够进行绘制热图。否则,列之间的数据大小相差太多,无法看出实际效果。
中心化处理后:
未中心化处理和中心化处理后的效果相同,所有的值之间还是相差很多。
标准化处理后:
标准化处理后,可以看出之间的差异,虽然进行标准化处理,但是并不影响每一列之间的差异。
4.8 merge函数
定义:Merge two data frames by common columns or row names
merge函数会将相同的部分进行组合:
参数:merge(x, y, by = intersect(names(x), names(y)),
x,y:要合并的数据框
by,by.x,by.y:指定依据什么合并数据框,默认为相同colname的列
all,all.x,all.y:指定x和y的行是否应该全部输出
sort by:by后指定的列是否排序
suffixes:指定不用于合并的列中拥有相同列名的后缀
incomparables:指定合并的列中,哪些值不需要进行合并(NULL or NA or 其他)
当两个数据框有相同的观测量(rowname或colname相同),但观测量下的观测值不同时,使用merge函数进行合并。通过“by=观测因子”,得到共有的观测值对应的其他观测量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 > x <- data.frame( k1 = c ( NA , NA , 3 , 4 , 5 ) , k2 = c ( 1 , NA , NA , 4 , 5 ) , data = 1 : 5 ) > x k1 k2 data 1 NA 1 1 2 NA NA 2 3 3 NA 3 4 4 4 4 5 5 5 5 > y <- data.frame( k1 = c ( NA , 2 , NA , 4 , 5 ) , k2 = c ( NA , NA , 3 , 4 , 5 ) , data = 1 : 5 ) > y k1 k2 data 1 NA NA 1 2 2 NA 2 3 NA 3 3 4 4 4 4 5 5 5 5 > rbind( x, y) k1 k2 data 1 NA 1 1 2 NA NA 2 3 3 NA 3 4 4 4 4 5 5 5 5 6 NA NA 1 7 2 NA 2 8 NA 3 3 9 4 4 4 10 5 5 5 > merge( x, y, by= "k1" ) k1 k2.x data.x k2.y data.y 1 4 4 4 4 4 2 5 5 5 5 5 3 NA 1 1 NA 1 4 NA 1 1 3 3 5 NA NA 2 NA 1 6 NA NA 2 3 3 > merge( x, y, by= "k2" ) k2 k1.x data.x k1.y data.y 1 4 4 4 4 4 2 5 5 5 5 5 3 NA NA 2 NA 1 4 NA NA 2 2 2 5 NA 3 3 NA 1 6 NA 3 3 2 2 > merge( x, y, by= "k2" , incomparables = T ) k2 k1.x data.x k1.y data.y 1 4 4 4 4 4 2 5 5 5 5 5 3 NA NA 2 NA 1 4 NA NA 2 2 2 5 NA 3 3 NA 1 6 NA 3 3 2 2 > merge( x, y, by= c ( "k1" , "k2" ) ) k1 k2 data.x data.y 1 4 4 4 4 2 5 5 5 5 3 NA NA 2 1
总结:merge会组合合并,merge(x,y,by="k2",incomparables = T)表示根据k2进行合并,incomparables表示丢掉NA的情况。merge(x,y,by=c("k1","k2"))表示同时合并k1,k2。
不推荐使用merge函数。
4.9 reshape2包
reshape2包功能更强大,学习难度大。
需要安装reshape2包。
1 2 > install.packages( "reshape2" ) > library( reshape2)
重塑数据,首先把宽数据融合(melt),以使每一行都只表示一个变量,然后把数据重塑(cast)为想要的任何形状。在重塑过程中,可以使用任何函数对数据进行整合,也可以把长格式转换为宽格式,这种操作类似于Excel的透视和逆透视。
在同一行,标识变量(一列或多列)能够唯一标识两个或多个变量的值,这种数据显示叫做数据的宽格式,也叫做宽数据 。
4.9.1 melt函数
使用方法:
1 melt( data, id.vars, measure.vars, variable.name= 'variable' , ..., na.rm= FALSE , value.name= 'value' , factorAsStrings= TRUE )
参数注释:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 > library( reshape2) > newdata <- airquality[ 1 : 10 , ] > newdata ozone solar.r wind temp month day 1 41 190 7.4 67 5 1 2 36 118 8.0 72 5 2 3 12 149 12.6 74 5 3 4 18 313 11.5 62 5 4 5 NA NA 14.3 56 5 5 6 28 NA 14.9 66 5 6 7 23 299 8.6 65 5 7 8 19 99 13.8 59 5 8 9 8 19 20.1 61 5 9 10 NA 194 8.6 69 5 10 > melt( newdata) No id variables; using all as measure variables variable value 1 ozone 41.0 2 ozone 36.0 3 ozone 12.0 4 ozone 18.0 5 ozone NA 6 ozone 28.0 7 ozone 23.0 8 ozone 19.0 9 ozone 8.0 10 ozone NA 11 solar.r 190.0 12 solar.r 118.0 13 solar.r 149.0 14 solar.r 313.0 15 solar.r NA 16 solar.r NA 17 solar.r 299.0 18 solar.r 99.0 19 solar.r 19.0 20 solar.r 194.0 21 wind 7.4 22 wind 8.0 23 wind 12.6 24 wind 11.5 25 wind 14.3 26 wind 14.9 27 wind 8.6 28 wind 13.8 29 wind 20.1 30 wind 8.6 31 temp 67.0 32 temp 72.0 33 temp 74.0 34 temp 62.0 35 temp 56.0 36 temp 66.0 37 temp 65.0 38 temp 59.0 39 temp 61.0 40 temp 69.0 41 month 5.0 42 month 5.0 43 month 5.0 44 month 5.0 45 month 5.0 46 month 5.0 47 month 5.0 48 month 5.0 49 month 5.0 50 month 5.0 51 day 1.0 52 day 2.0 53 day 3.0 54 day 4.0 55 day 5.0 56 day 6.0 57 day 7.0 58 day 8.0 59 day 9.0 60 day 10.0
总结:melt函数将所有的向量在一列表示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 > melt( newdata, id.vars = c ( "month" , "day" ) ) month day variable value 1 5 1 ozone 41.0 2 5 2 ozone 36.0 3 5 3 ozone 12.0 4 5 4 ozone 18.0 5 5 5 ozone NA 6 5 6 ozone 28.0 7 5 7 ozone 23.0 8 5 8 ozone 19.0 9 5 9 ozone 8.0 10 5 10 ozone NA 11 5 1 solar.r 190.0 12 5 2 solar.r 118.0 13 5 3 solar.r 149.0 14 5 4 solar.r 313.0 15 5 5 solar.r NA 16 5 6 solar.r NA 17 5 7 solar.r 299.0 18 5 8 solar.r 99.0 19 5 9 solar.r 19.0 20 5 10 solar.r 194.0 21 5 1 wind 7.4 22 5 2 wind 8.0 23 5 3 wind 12.6 24 5 4 wind 11.5 25 5 5 wind 14.3 26 5 6 wind 14.9 27 5 7 wind 8.6 28 5 8 wind 13.8 29 5 9 wind 20.1 30 5 10 wind 8.6 31 5 1 temp 67.0 32 5 2 temp 72.0 33 5 3 temp 74.0 34 5 4 temp 62.0 35 5 5 temp 56.0 36 5 6 temp 66.0 37 5 7 temp 65.0 38 5 8 temp 59.0 39 5 9 temp 61.0 40 5 10 temp 69.0
总结:melt中参数id.vars表示不合并哪些列。
此外还有dcast、acast函数
reshape2包比较复杂,tidyr包和dplyr包两者组合可以替换reshape2包,相对来说更简单。
4.10 tidyr包
需要安装tidyr包
1 2 > install.packages( "tidyr" ) > library( tidyr)
Tidy data数据指的是可以根据一个行名和一个列名可以确定一个值。
gather函数类似于melt函数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 > tdata <- mtcars[ 1 : 10 , 1 : 3 ] > tdata mpg cyl disp Mazda RX4 21.0 6 160.0 Mazda RX4 Wag 21.0 6 160.0 Datsun 710 22.8 4 108.0 Hornet 4 Drive 21.4 6 258.0 Hornet Sportabout 18.7 8 360.0 Valiant 18.1 6 225.0 Duster 360 14.3 8 360.0 Merc 240 D 24.4 4 146.7 Merc 230 22.8 4 140.8 Merc 280 19.2 6 167.6 > tdata <- data.frame( names = rownames( tdata) , tdata) > tdata names mpg cyl disp Mazda RX4 Mazda RX4 21.0 6 160.0 Mazda RX4 Wag Mazda RX4 Wag 21.0 6 160.0 Datsun 710 Datsun 710 22.8 4 108.0 Hornet 4 Drive Hornet 4 Drive 21.4 6 258.0 Hornet Sportabout Hornet Sportabout 18.7 8 360.0 Valiant Valiant 18.1 6 225.0 Duster 360 Duster 360 14.3 8 360.0 Merc 240 D Merc 240 D 24.4 4 146.7 Merc 230 Merc 230 22.8 4 140.8 Merc 280 Merc 280 19.2 6 167.6 > gather( tdata, key = "Key" , value = "Value" , cyl, disp, - mpg) names mpg Key Value 1 Mazda RX4 21.0 cyl 6.0 2 Mazda RX4 Wag 21.0 cyl 6.0 3 Datsun 710 22.8 cyl 4.0 4 Hornet 4 Drive 21.4 cyl 6.0 5 Hornet Sportabout 18.7 cyl 8.0 6 Valiant 18.1 cyl 6.0 7 Duster 360 14.3 cyl 8.0 8 Merc 240 D 24.4 cyl 4.0 9 Merc 230 22.8 cyl 4.0 10 Merc 280 19.2 cyl 6.0 11 Mazda RX4 21.0 disp 160.0 12 Mazda RX4 Wag 21.0 disp 160.0 13 Datsun 710 22.8 disp 108.0 14 Hornet 4 Drive 21.4 disp 258.0 15 Hornet Sportabout 18.7 disp 360.0 16 Valiant 18.1 disp 225.0 17 Duster 360 14.3 disp 360.0 18 Merc 240 D 24.4 disp 146.7 19 Merc 230 22.8 disp 140.8 20 Merc 280 19.2 disp 167.6
总结:mpg前面的符号-表示不需要转换的列,如果列的名字容易出错,可以直接写列的编号,如下所示:
1 2 > gather( tdata, key = "Key" , value = "Value" , 3 : 4 ) > gather( tdata, key = "Key" , value = "Value" , 2 , 4 )
spread函数和gather函数作用正好相反。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 > gdata <- gather( tdata, key = "Key" , value = "Value" , 2 : 4 ) > gdata names Key Value 1 Mazda RX4 mpg 21.0 2 Mazda RX4 Wag mpg 21.0 3 Datsun 710 mpg 22.8 4 Hornet 4 Drive mpg 21.4 5 Hornet Sportabout mpg 18.7 6 Valiant mpg 18.1 7 Duster 360 mpg 14.3 8 Merc 240 D mpg 24.4 9 Merc 230 mpg 22.8 10 Merc 280 mpg 19.2 11 Mazda RX4 cyl 6.0 12 Mazda RX4 Wag cyl 6.0 13 Datsun 710 cyl 4.0 14 Hornet 4 Drive cyl 6.0 15 Hornet Sportabout cyl 8.0 16 Valiant cyl 6.0 17 Duster 360 cyl 8.0 18 Merc 240 D cyl 4.0 19 Merc 230 cyl 4.0 20 Merc 280 cyl 6.0 21 Mazda RX4 disp 160.0 22 Mazda RX4 Wag disp 160.0 23 Datsun 710 disp 108.0 24 Hornet 4 Drive disp 258.0 25 Hornet Sportabout disp 360.0 26 Valiant disp 225.0 27 Duster 360 disp 360.0 28 Merc 240 D disp 146.7 29 Merc 230 disp 140.8 30 Merc 280 disp 167.6 > spread( gdata, key = "Key" , value = "Value" ) names cyl disp mpg 1 Datsun 710 4 108.0 22.8 2 Duster 360 8 360.0 14.3 3 Hornet 4 Drive 6 258.0 21.4 4 Hornet Sportabout 8 360.0 18.7 5 Mazda RX4 6 160.0 21.0 6 Mazda RX4 Wag 6 160.0 21.0 7 Merc 230 4 140.8 22.8 8 Merc 240 D 4 146.7 24.4 9 Merc 280 6 167.6 19.2 10 Valiant 6 225.0 18.1
separate函数和unite函数对应,separate函数根据列进行分割,可以将一列拆分成多列,而unite函数则是合并列,如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 > df <- data.frame( x= c ( NA , "a.b" , "a.d" , "b.c" ) ) > df x 1 < NA > 2 a.b3 a.d4 b.c> separate( df, col= x, into = c ( "A" , "B" ) ) A B 1 < NA > < NA > 2 a b3 a d4 b c
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 ddf <- data.frame( x= c ( NA , "a.b-c" , "a-d" , "b-c" ) ) > ddf x 1 < NA > 2 a.b- c 3 a- d4 b- c > separate( ddf, col= x, into = c ( "A" , "B" ) ) A B 1 < NA > < NA > 2 a b3 a d4 b c Warning message: Expected 2 pieces. Additional pieces discarded in 1 rows [ 2 ] . > x <- separate( ddf, col= x, into = c ( "A" , "B" ) , sep = "-" ) > x A B 1 < NA > < NA > 2 a.b c 3 a d4 b c > unite( x, col = "AB" , A, B, sep = "-" ) AB 1 NA - NA 2 a.b- c 3 a- d4 b- c
4.11 dplyr包
需要安装dplyr包
1 2 > install.packages( "dplyr" ) > library( dplyr)
dplyr包功能强大,很多数据转换都可以用dplyr轻松完成,不仅可以对单个表格进行操作,也可以对双表格进行操作。可以通过ls函数查看dplyr包中的函数:
由于dplyr包的函数太多,为了避免和其他包重名,需要在函数前面加上包的名字,例如:dplyr::filter。
filter函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 > dplyr:: filter( iris, Sepal.Length> 7 ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 7.1 3.0 5.9 2.1 virginica2 7.6 3.0 6.6 2.1 virginica3 7.3 2.9 6.3 1.8 virginica4 7.2 3.6 6.1 2.5 virginica5 7.7 3.8 6.7 2.2 virginica6 7.7 2.6 6.9 2.3 virginica7 7.7 2.8 6.7 2.0 virginica8 7.2 3.2 6.0 1.8 virginica9 7.2 3.0 5.8 1.6 virginica10 7.4 2.8 6.1 1.9 virginica11 7.9 3.8 6.4 2.0 virginica12 7.7 3.0 6.1 2.3 virginica
distinct表示去除重复行,类似于unique的功能。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > dplyr:: distinct( rbind( iris[ 1 : 10 , ] , iris[ 1 : 15 , ] ) ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa2 4.9 3.0 1.4 0.2 setosa3 4.7 3.2 1.3 0.2 setosa4 4.6 3.1 1.5 0.2 setosa5 5.0 3.6 1.4 0.2 setosa6 5.4 3.9 1.7 0.4 setosa7 4.6 3.4 1.4 0.3 setosa8 5.0 3.4 1.5 0.2 setosa9 4.4 2.9 1.4 0.2 setosa10 4.9 3.1 1.5 0.1 setosa11 5.4 3.7 1.5 0.2 setosa12 4.8 3.4 1.6 0.2 setosa13 4.8 3.0 1.4 0.1 setosa14 4.3 3.0 1.1 0.1 setosa15 5.8 4.0 1.2 0.2 setosa
slice函数表示取出某些行:
1 2 3 4 5 6 7 8 > dplyr:: slice( iris, 10 : 15 ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 4.9 3.1 1.5 0.1 setosa2 5.4 3.7 1.5 0.2 setosa3 4.8 3.4 1.6 0.2 setosa4 4.8 3.0 1.4 0.1 setosa5 4.3 3.0 1.1 0.1 setosa6 5.8 4.0 1.2 0.2 setosa
sample_n函数表示随机取样,随机抽取某些行:
1 2 3 4 5 6 7 8 9 10 11 12 > dplyr:: sample_n( iris, 10 ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 4.8 3.4 1.6 0.2 setosa2 6.9 3.2 5.7 2.3 virginica3 5.1 3.3 1.7 0.5 setosa4 7.0 3.2 4.7 1.4 versicolor5 6.4 3.2 4.5 1.5 versicolor6 5.8 2.7 5.1 1.9 virginica7 5.0 3.2 1.2 0.2 setosa8 4.6 3.4 1.4 0.3 setosa9 6.0 2.2 5.0 1.5 virginica10 6.3 2.8 5.1 1.5 virginica
sample_frac表示按比例随机选取:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > dplyr:: sample_frac( iris, 0.1 ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 6.6 3.0 4.4 1.4 versicolor2 6.3 2.5 5.0 1.9 virginica3 5.2 3.5 1.5 0.2 setosa4 4.4 3.0 1.3 0.2 setosa5 6.6 2.9 4.6 1.3 versicolor6 4.9 3.1 1.5 0.2 setosa7 4.9 2.5 4.5 1.7 virginica8 4.9 3.1 1.5 0.1 setosa9 5.9 3.2 4.8 1.8 versicolor10 6.1 3.0 4.6 1.4 versicolor11 6.1 2.8 4.7 1.2 versicolor12 6.9 3.2 5.7 2.3 virginica13 5.5 4.2 1.4 0.2 setosa14 5.7 3.0 4.2 1.2 versicolor15 5.8 4.0 1.2 0.2 setosa
arrange函数用于排序,默认从小到大进行排序:
1 2 3 4 5 6 7 8 > head( dplyr:: arrange( iris, Sepal.Length) ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 4.3 3.0 1.1 0.1 setosa2 4.4 2.9 1.4 0.2 setosa3 4.4 3.0 1.3 0.2 setosa4 4.4 3.2 1.3 0.2 setosa5 4.5 2.3 1.3 0.3 setosa6 4.6 3.1 1.5 0.2 setosa
如果加上desc表示根据从大到小进行排序:
1 2 3 4 5 6 7 8 > head( dplyr:: arrange( iris, desc( Sepal.Length) ) ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 7.9 3.8 6.4 2.0 virginica2 7.7 3.8 6.7 2.2 virginica3 7.7 2.6 6.9 2.3 virginica4 7.7 2.8 6.7 2.0 virginica5 7.7 3.0 6.1 2.3 virginica6 7.6 3.0 6.6 2.1 virginica
dplyr包也有数据框取子集的功能,可以利用select函数,相关示例通过?select命令查看。
summarise函数用来统计:
1 2 3 4 5 6 > summarise( iris, avg= mean( Sepal.Length) ) avg 1 5.843333 > summarise( iris, sum = sum ( Sepal.Length) ) sum 1 876.5
链式操作符
两个百分号中间夹着一个大于号,称为链式操作符,它功能是用于实现将一个函数的输出传递给下一个函数,作为下一个函数的输入。
在Rstudio中可以使用ctrl + shift + M快捷键输出出来。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > head( mtcars, 20 ) mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4 Merc 280 C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4 Merc 450 SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3 Merc 450 SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3 Merc 450 SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3 Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1 > head( mtcars, 20 ) %>% tail( 10 ) mpg cyl disp hp drat wt qsec vs am gear carb Merc 280 C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4 Merc 450 SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3 Merc 450 SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3 Merc 450 SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3 Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1
group_by函数可以对函数进行分组:通过Species这一列对鸢尾花进行分组,分为三组:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 > dplyr:: group_by( iris, Species) Sepal.Length Sepal.Width Petal.Length Petal.Width Species < dbl> < dbl> < dbl> < dbl> < fct> 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa > iris %>% group_by( Species) Sepal.Length Sepal.Width Petal.Length Petal.Width Species < dbl> < dbl> < dbl> < dbl> < fct> 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa > iris %>% group_by( Species) %>% summarise( ) Species < fct> 1 setosa 2 versicolor3 virginica > iris %>% group_by( Species) %>% summarise( avg= mean( Sepal.Width) ) Species avg < fct> < dbl> 1 setosa 3.43 2 versicolor 2.77 3 virginica 2.97 > iris %>% group_by( Species) %>% summarise( avg= mean( Sepal.Width) ) %>% arrange( avg) Species avg < fct> < dbl> 1 versicolor 2.77 2 virginica 2.97 3 setosa 3.43
mutate函数可以添加新的变量:
1 2 3 4 5 6 7 8 > head( dplyr:: mutate( iris, new = Sepal.Length+ Petal.Length) ) Sepal.Length Sepal.Width Petal.Length Petal.Width Species new 1 5.1 3.5 1.4 0.2 setosa 6.5 2 4.9 3.0 1.4 0.2 setosa 6.3 3 4.7 3.2 1.3 0.2 setosa 6.0 4 4.6 3.1 1.5 0.2 setosa 6.1 5 5.0 3.6 1.4 0.2 setosa 6.4 6 5.4 3.9 1.7 0.4 setosa 7.1
下面对双表格进行操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 > a= data.frame( x1= c ( "A" , "B" , "C" ) , x2= c ( 1 , 2 , 3 ) ) > a x1 x2 1 A 1 2 B 2 3 C 3 > b= data.frame( x1= c ( "A" , "B" , "D" ) , x3= c ( T , F , T ) ) > b x1 x3 1 A TRUE 2 B FALSE 3 D TRUE > dplyr:: left_join( a, b, by= "x1" ) x1 x2 x3 1 A 1 TRUE 2 B 2 FALSE 3 C 3 NA > dplyr:: right_join( a, b, by= "x1" ) x1 x2 x3 1 A 1 TRUE 2 B 2 FALSE 3 D NA TRUE > dplyr:: full_join( a, b, by= "x1" ) x1 x2 x3 1 A 1 TRUE 2 B 2 FALSE 3 C 3 NA 4 D NA TRUE > dplyr:: semi_join( a, b, by= "x1" ) x1 x2 1 A 1 2 B 2 > dplyr:: anti_join( a, b, by= "x1" ) x1 x2 1 C 3 > dplyr:: anti_join( b, a, by= "x1" ) x1 x3 1 D TRUE
intersect函数用来取交集:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 > mtcars <- mutate( mtcars, Model= rownames( mtcars) ) > first <- slice( mtcars, 1 : 6 ) > first mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1 Valiant > second <- slice( mtcars, 5 : 15 ) > second <- slice( mtcars, 4 : 9 ) > second mpg cyl disp hp drat wt qsec vs am gear carb Model Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Valiant Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Duster 360 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 Merc 240 D Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 Merc 230 > intersect( first, second) mpg cyl disp hp drat wt qsec vs am gear carb Model Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1 Valiant
union取非冗余的并集,即自动剔除冗余部分。union_all只是简单的并集,不会提出冗余部分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > dplyr:: union_all( first, second) mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 Hornet 4 Drive...4 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout...5 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant...6 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Valiant Hornet 4 Drive...7 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout...8 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant...9 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Valiant Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Duster 360 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 Merc 240 D Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 Merc 230 > dplyr:: union( first, second) mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Valiant Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Duster 360 Merc 240 D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 Merc 240 D Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 Merc 230
setdiff取第一个参数的补集
1 2 3 4 5 6 7 8 9 10 > setdiff( first, second) mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 > setdiff( second, first) mpg cyl disp hp drat wt qsec vs am gear carb Model Duster 360 14.3 8 360.0 245 3.21 3.57 15.84 0 0 3 4 Duster 360 Merc 240 D 24.4 4 146.7 62 3.69 3.19 20.00 1 0 4 2 Merc 240 D Merc 230 22.8 4 140.8 95 3.92 3.15 22.90 1 0 4 2 Merc 230
5 R函数
R函数是R语言重要组成部分
比如用lm函数进行线性回归分析:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > state <- as.data.frame( state.x77[ , c ( "Murder" , "Population" , "Illiteracy" , "Income" , "Frost" ) ] ) > fit<- lm ( Murder ~ Population+ Illiteracy+ Income+ Frost, data= state) > fitCall: lm( formula = Murder ~ Population + Illiteracy + Income + Frost, data = state) Coefficients: ( Intercept) Population Illiteracy Income Frost 1.235e+00 2.237e-04 4.143e+00 6.442e-05 5.813e-04 > summary( fit) Call: lm( formula = Murder ~ Population + Illiteracy + Income + Frost, data = state) Residuals: Min 1 Q Median 3 Q Max - 4.7960 - 1.6495 - 0.0811 1.4815 7.6210 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) 1.235e+00 3.866e+00 0.319 0.7510 Population 2.237e-04 9.052e-05 2.471 0.0173 * Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 * * * Income 6.442e-05 6.837e-04 0.094 0.9253 Frost 5.813e-04 1.005e-02 0.058 0.9541 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.535 on 45 degrees of freedom Multiple R- squared: 0.567 , Adjusted R- squared: 0.5285 F - statistic: 14.73 on 4 and 45 DF, p- value: 9.133e-08
绘图过程中,如果是向量和向量绘制的就是散点图,如果是向量和因子绘制的就是条形图。
输入数据类型:
向量:sum、mean、sd、range、median、sort、order
矩阵或数据框:cbind、rbind
数字矩阵:heatmap
5.1 选项参数
输入控制部分;
输出控制部分;
调节部分。
file:接一个文件;
data:一般指要输入一个数据框;
x:表示单独的一个对象,一般都是向量,也可以是矩阵或者列表;
x和y:函数需要两个输入变量;
x,y,z:函数需要三个输入变量;
formula:公式;y ~ x表示x和y相关。
na.rm:删除缺失值;
……
有时候会存在三个点…,表示和其他函数功能重合,功能通用。有时候三个点在前面表示可以合并任意的对象,比如data.frame函数:
调节参数 :
color:选项和明显用来控制颜色
select:与选择有关
font:与字体有关
font.axis:就是坐标轴的字体
lty:是line type,线型
lwd:是line width,线宽
method:软件算法
……
选项接受哪些参数 :
main:字符串,不能是向量
na.rm:TRUE或者FALSE
axis:side参数只能是1到4,控制坐标轴的方向
fig:包含四个元素的向量,控制图形区域的位置
……
5.2 数学统计函数
概率论
概率论是统计学的基础,R有许多用于处理概率,概率分布以及随机变量的函数。R对每一个概率分布都有一个简称,这个名称用于识别与分布相联系的函数。这部分涉及到很多统计学基础的理论知识,比如随机试验,样本空间,对立与互斥,随机事件与必然事件,概率密度,概率分布等。
d:概率密度函数
p:分布函数
q:分布函数的反函数
r:产生相同分布的随机数
比如正态分布:
1 2 3 4 dnorm( x, mean = 0 , sd = 1 , log = FALSE ) pnorm( q, mean = 0 , sd = 1 , lower.tail = TRUE , log.p = FALSE ) qnorm( p, mean = 0 , sd = 1 , lower.tail = TRUE , log.p = FALSE ) rnorm( n, mean = 0 , sd = 1 )
rnorm(n, mean = 0, sd = 1)表示产生n个均值为0,方差为1的随机数。
在每个函数前面加上d、p、q、r就构成了函数名。
分布名称
分布
R中的名称
附加参数
Beta分布
beta
beta
shape1, shape2, ncp
二项分布
binomial
binom
size, prob
柯西分布
Cauchy
cauchy
location, scale
(非中心)卡方分布
chi-squared
chisq
df, ncp
指数分布
exponential
exp
rate
F分布
F分布
F
f
Gamma分布
gamma
gamma
shape, scale
几何分布
geometric
geom
prob
超几何分布
hypergeometric
hyper
m, n, k
对数正态分布
log-normal
lnorm
meanlog, sdlog
Logistic分布
logistic
logis
location, scale
负二项分布
negative binomial
nbinom
size, prob
正态分布
normal
norm
mean, sd
泊松分布
Poisson
pois
lambda
t分布
Student’s t
t
df, ncp
均匀分布
uniform
unif
min, max
Weibull分布
Weibull
weibull
shape, scale
Wilcoxon秩和分布
Wilcoxon
wilcox
m, n
Wilcoxon符号秩分布
SignRank
signrank
n
对数正态分布
Lognormal
lnorm
meanlog, sdlog
runif:生成0-1之间的随机数。
1 2 3 4 5 > runif( 10 , min = 1 , max = 100 ) [ 1 ] 36.846837 5.020477 21.099430 97.208172 18.753216 78.498546 79.735780 48.014668 74.315821 36.491041 > x <- rnorm( n= 10 , mean= 15 , sd= 2 ) > x [ 1 ] 15.50968 15.79180 14.99966 17.11203 15.27945 17.26010 13.09434 13.34831 12.28590 14.21707
通过set.seed则每次运行状态和上次使用set.seed后同样次数下的运行结果相同:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > set.seed( 666 ) > runif( 10 ) [ 1 ] 0.77436849 0.19722419 0.97801384 0.20132735 0.36124443 0.74261194 0.97872844 0.49811371 0.01331584 [ 10 ] 0.25994613 > runif( 10 ) [ 1 ] 0.77589308 0.01637905 0.09574478 0.14216354 0.21112624 0.81125644 0.03654720 0.89163741 0.48323641 [ 10 ] 0.46666453 > set.seed( 666 ) > runif( 10 ) [ 1 ] 0.77436849 0.19722419 0.97801384 0.20132735 0.36124443 0.74261194 0.97872844 0.49811371 0.01331584 [ 10 ] 0.25994613 > runif( 10 ) [ 1 ] 0.77589308 0.01637905 0.09574478 0.14216354 0.21112624 0.81125644 0.03654720 0.89163741 0.48323641 [ 10 ] 0.46666453
5.3 描述性统计函数
5.3.1 整体描述函数
1 2 3 4 5 6 7 8 9 10 11 > myvars <- mtcars[ c ( "mpg" , "hp" , "wt" , "am" ) ] > summary( myvars) mpg hp wt am Min. : 10.40 Min. : 52.0 Min. : 1.513 Min. : 0.0000 1 st Qu.: 15.43 1 st Qu.: 96.5 1 st Qu.: 2.581 1 st Qu.: 0.0000 Median : 19.20 Median : 123.0 Median : 3.325 Median : 0.0000 Mean : 20.09 Mean : 146.7 Mean : 3.217 Mean : 0.4062 3 rd Qu.: 22.80 3 rd Qu.: 180.0 3 rd Qu.: 3.610 3 rd Qu.: 1.0000 Max. : 33.90 Max. : 335.0 Max. : 5.424 Max. : 1.0000 > fivenum( myvars$ hp) [ 1 ] 52 96 123 180 335
总结:通过summary函数可以进行最大值,最小值,均值等的统计。fivenum和summary类似,返回最小值、lower-hinge, 中位数, upper-hinge, 最大值。
类似的包还有Hmisc包中的describe函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > describe( myvars) myvars 4 Variables 32 Observations - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - mpg n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 32 0 25 0.999 20.09 6.796 12.00 14.34 15.43 19.20 22.80 30.09 .95 31.30 lowest : 10.4 13.3 14.3 14.7 15.0 , highest: 26.0 27.3 30.4 32.4 33.9 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - hp n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 32 0 22 0.997 146.7 77.04 63.65 66.00 96.50 123.00 180.00 243.50 .95 253.55 lowest : 52 62 65 66 91 , highest: 215 230 245 264 335 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - wt n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 32 0 29 0.999 3.217 1.089 1.736 1.956 2.581 3.325 3.610 4.048 .95 5.293 lowest : 1.513 1.615 1.835 1.935 2.140 , highest: 3.845 4.070 5.250 5.345 5.424 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - am n missing distinct Info Sum Mean Gmd 32 0 2 0.724 13 0.4062 0.498 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
可以返回观测的数量、缺失值和唯一值的数目、以及平均值、分位数,五个最大值和五个最小值
再比如pastecs包中的desc函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 > stat.desc( myvars) mpg hp wt am nbr.val 32.0000000 32.0000000 32.0000000 32.00000000 nbr.null 0.0000000 0.0000000 0.0000000 19.00000000 nbr.na 0.0000000 0.0000000 0.0000000 0.00000000 min 10.4000000 52.0000000 1.5130000 0.00000000 max 33.9000000 335.0000000 5.4240000 1.00000000 range 23.5000000 283.0000000 3.9110000 1.00000000 sum 642.9000000 4694.0000000 102.9520000 13.00000000 median 19.2000000 123.0000000 3.3250000 0.00000000 mean 20.0906250 146.6875000 3.2172500 0.40625000 SE.mean 1.0654240 12.1203173 0.1729685 0.08820997 CI.mean.0.95 2.1729465 24.7195501 0.3527715 0.17990541 var 36.3241028 4700.8669355 0.9573790 0.24899194 std.dev 6.0269481 68.5628685 0.9784574 0.49899092 coef.var 0.2999881 0.4674077 0.3041285 1.22828533 > stat.desc( myvars, basic = T ) mpg hp wt am nbr.val 32.0000000 32.0000000 32.0000000 32.00000000 nbr.null 0.0000000 0.0000000 0.0000000 19.00000000 nbr.na 0.0000000 0.0000000 0.0000000 0.00000000 min 10.4000000 52.0000000 1.5130000 0.00000000 max 33.9000000 335.0000000 5.4240000 1.00000000 range 23.5000000 283.0000000 3.9110000 1.00000000 sum 642.9000000 4694.0000000 102.9520000 13.00000000 median 19.2000000 123.0000000 3.3250000 0.00000000 mean 20.0906250 146.6875000 3.2172500 0.40625000 SE.mean 1.0654240 12.1203173 0.1729685 0.08820997 CI.mean.0.95 2.1729465 24.7195501 0.3527715 0.17990541 var 36.3241028 4700.8669355 0.9573790 0.24899194 std.dev 6.0269481 68.5628685 0.9784574 0.49899092 coef.var 0.2999881 0.4674077 0.3041285 1.22828533 > stat.desc( myvars, desc = T ) mpg hp wt am nbr.val 32.0000000 32.0000000 32.0000000 32.00000000 nbr.null 0.0000000 0.0000000 0.0000000 19.00000000 nbr.na 0.0000000 0.0000000 0.0000000 0.00000000 min 10.4000000 52.0000000 1.5130000 0.00000000 max 33.9000000 335.0000000 5.4240000 1.00000000 range 23.5000000 283.0000000 3.9110000 1.00000000 sum 642.9000000 4694.0000000 102.9520000 13.00000000 median 19.2000000 123.0000000 3.3250000 0.00000000 mean 20.0906250 146.6875000 3.2172500 0.40625000 SE.mean 1.0654240 12.1203173 0.1729685 0.08820997 CI.mean.0.95 2.1729465 24.7195501 0.3527715 0.17990541 var 36.3241028 4700.8669355 0.9573790 0.24899194 std.dev 6.0269481 68.5628685 0.9784574 0.49899092 coef.var 0.2999881 0.4674077 0.3041285 1.22828533 > stat.desc( myvars, norm = T ) mpg hp wt am nbr.val 32.0000000 32.00000000 32.00000000 3.200000e+01 nbr.null 0.0000000 0.00000000 0.00000000 1.900000e+01 nbr.na 0.0000000 0.00000000 0.00000000 0.000000e+00 min 10.4000000 52.00000000 1.51300000 0.000000e+00 max 33.9000000 335.00000000 5.42400000 1.000000e+00 range 23.5000000 283.00000000 3.91100000 1.000000e+00 sum 642.9000000 4694.00000000 102.95200000 1.300000e+01 median 19.2000000 123.00000000 3.32500000 0.000000e+00 mean 20.0906250 146.68750000 3.21725000 4.062500e-01 SE.mean 1.0654240 12.12031731 0.17296847 8.820997e-02 CI.mean.0.95 2.1729465 24.71955013 0.35277153 1.799054e-01 var 36.3241028 4700.86693548 0.95737897 2.489919e-01 std.dev 6.0269481 68.56286849 0.97845744 4.989909e-01 coef.var 0.2999881 0.46740771 0.30412851 1.228285e+00 skewness 0.6106550 0.72602366 0.42314646 3.640159e-01 skew.2SE 0.7366922 0.87587259 0.51048252 4.391476e-01 kurtosis - 0.3727660 - 0.13555112 - 0.02271075 - 1.924741e+00 kurt.2SE - 0.2302812 - 0.08373853 - 0.01402987 - 1.189035e+00 normtest.W 0.9475647 0.93341934 0.94325772 6.250744e-01 normtest.p 0.1228814 0.04880824 0.09265499 7.836354e-08
在psych包中,同样包含describe函数,可以计算非缺失值的数量。
1 2 3 4 5 6 7 8 9 10 11 12 > describe( myvars) vars n mean sd median trimmed mad min max range skew kurtosis se mpg 1 32 20.09 6.03 19.20 19.70 5.41 10.40 33.90 23.50 0.61 - 0.37 1.07 hp 2 32 146.69 68.56 123.00 141.19 77.10 52.00 335.00 283.00 0.73 - 0.14 12.12 wt 3 32 3.22 0.98 3.33 3.15 0.77 1.51 5.42 3.91 0.42 - 0.02 0.17 am 4 32 0.41 0.50 0.00 0.38 0.00 0.00 1.00 1.00 0.36 - 1.92 0.09 > describe( myvars, trim = 0.1 ) vars n mean sd median trimmed mad min max range skew kurtosis se mpg 1 32 20.09 6.03 19.20 19.70 5.41 10.40 33.90 23.50 0.61 - 0.37 1.07 hp 2 32 146.69 68.56 123.00 141.19 77.10 52.00 335.00 283.00 0.73 - 0.14 12.12 wt 3 32 3.22 0.98 3.33 3.15 0.77 1.51 5.42 3.91 0.42 - 0.02 0.17 am 4 32 0.41 0.50 0.00 0.38 0.00 0.00 1.00 1.00 0.36 - 1.92 0.09
同样可以计算非缺失值的数量、平均数、中位数、最大值、最小值等。trim = 0.1表示去掉最低和最高10%的部分。
后载入的包中如果函数名字和前面载入的包中函数名字重复,会将前面载入的包的函数覆盖,如果想重新使用前面载入的包的函数,可以选择重新载入前面载入的包。也可以使用包名::函数名的方法使用前面的包中的函数。
5.3.2 分组描述函数
stats包中可以通过aggregate进行分组描述数据:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > aggregate( Cars93[ c ( "Min.Price" , "Price" , "Max.Price" , "MPG.city" ) ] , by= list ( Cars93$ Origin) , mean) Group.1 Min.Price Price Max.Price MPG.city 1 USA 16.53542 18.57292 20.62708 20.95833 2 non- USA 17.75556 20.50889 23.25556 23.86667 > aggregate( Cars93[ c ( "Min.Price" , "Price" , "Max.Price" , "MPG.city" ) ] , by= list ( Origin= Cars93$ Origin, Manufacturer= Cars93$ Manufacturer) , mean) Origin Manufacturer Min.Price Price Max.Price MPG.city 1 non- USA Acura 21.05000 24.90000 28.750 21.50000 2 non- USA Audi 28.35000 33.40000 38.450 19.50000 3 non- USA BMW 23.70000 30.00000 36.200 22.00000 4 USA Buick 20.75000 21.62500 22.550 19.00000 5 USA Cadillac 35.25000 37.40000 39.500 16.00000 ... 26 non- USA Saab 20.30000 28.70000 37.100 20.00000 27 USA Saturn 9.20000 11.10000 12.900 28.00000 28 non- USA Subaru 11.36667 12.93333 14.500 27.00000 29 non- USA Suzuki 7.30000 8.60000 10.000 39.00000 30 non- USA Toyota 14.02500 17.27500 20.550 24.25000 31 non- USA Volkswagen 16.45000 18.02500 19.575 20.25000 32 non- USA Volvo 23.30000 24.70000 26.000 20.50000
doBy包中summaryBy函数也可以进行分组描述数据:
1 2 3 4 5 > library( doBy) > summaryBy( mpg+ hp+ wt ~ am, data= myvars, FUN= mean) am mpg.mean hp.mean wt.mean 1 0 17.14737 160.2632 3.768895 2 1 24.39231 126.8462 2.411000
psych包中的describeBy函数可以进行分组描述数据,但是给出的统计值都是自定义不变的,无法给出自定义的函数的统计值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > describeBy( myvars, list ( am= mtcars$ am) ) Descriptive statistics by group am: 0 vars n mean sd median trimmed mad min max range skew kurtosis se mpg 1 19 17.15 3.83 17.30 17.12 3.11 10.40 24.40 14.00 0.01 - 0.80 0.88 hp 2 19 160.26 53.91 175.00 161.06 77.10 62.00 245.00 183.00 - 0.01 - 1.21 12.37 wt 3 19 3.77 0.78 3.52 3.75 0.45 2.46 5.42 2.96 0.98 0.14 0.18 am 4 19 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 NaN NaN 0.00 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - am: 1 vars n mean sd median trimmed mad min max range skew kurtosis se mpg 1 13 24.39 6.17 22.80 24.38 6.67 15.00 33.90 18.90 0.05 - 1.46 1.71 hp 2 13 126.85 84.06 109.00 114.73 63.75 52.00 335.00 283.00 1.36 0.56 23.31 wt 3 13 2.41 0.62 2.32 2.39 0.68 1.51 3.57 2.06 0.21 - 1.17 0.17 am 4 13 1.00 0.00 1.00 1.00 0.00 1.00 1.00 0.00 NaN NaN 0.00
5.4 频数统计函数
因子是专门用来分组的,分组后才能进行频数的统计。
如果数据本身就是因子,则直接可以进行分组。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 > mtcars$ cyl <- as.factor( c ( mtcars$ cyl) ) > mtcars$ cyl [ 1 ] 6 6 4 6 8 6 8 4 4 6 6 8 8 8 8 8 8 4 4 4 4 8 8 8 8 4 4 4 8 6 8 4 Levels: 4 6 8 > mtcars mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 ... Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Ferrari Dino Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Maserati Bora Volvo 142 E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 Volvo 142 E > split( mtcars, mtcars$ cyl) $ `4 ` mpg cyl disp hp drat wt qsec vs am gear carb Model Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1 Datsun 710 Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2 Merc 240D Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2 Merc 230 Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1 Fiat 128 Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2 Honda Civic Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1 Toyota Corolla Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1 Toyota Corona Fiat X1-9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1 Fiat X1-9 Porsche 914-2 26.0 4 120.3 91 4.43 2.140 16.70 0 1 5 2 Porsche 914-2 Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2 Lotus Europa Volvo 142E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2 Volvo 142E $`6` mpg cyl disp hp drat wt qsec vs am gear carb Model Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4 Mazda RX4 Wag Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1 Hornet 4 Drive Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1 Valiant Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4 Merc 280 Merc 280C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4 Merc 280C Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6 Ferrari Dino $`8` mpg cyl disp hp drat wt qsec vs am gear carb Model Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2 Hornet Sportabout Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4 Duster 360 Merc 450SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3 Merc 450SE Merc 450SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3 Merc 450SL Merc 450SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3 Merc 450SLC Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4 Cadillac Fleetwood Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4 Lincoln Continental Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4 Chrysler Imperial Dodge Challenger 15.5 8 318.0 150 2.76 3.520 16.87 0 0 3 2 Dodge Challenger AMC Javelin 15.2 8 304.0 150 3.15 3.435 17.30 0 0 3 2 AMC Javelin Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4 Camaro Z28 Pontiac Firebird 19.2 8 400.0 175 3.08 3.845 17.05 0 0 3 2 Pontiac Firebird Ford Pantera L 15.8 8 351.0 264 4.22 3.170 14.50 0 1 5 4 Ford Pantera L Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8 Maserati Bora
如果不是明显的因子,可以使用cut函数进行切割:
1 2 3 4 5 6 7 8 9 10 11 12 13 > cut( mtcars$ mpg, c ( seq( 10 , 50 , 10 ) ) ) [ 1 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 20 , 30 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 20 , 30 ] ( 20 , 30 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] [ 14 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 30 , 40 ] ( 30 , 40 ] ( 30 , 40 ] ( 20 , 30 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 20 , 30 ] [ 27 ] ( 20 , 30 ] ( 30 , 40 ] ( 10 , 20 ] ( 10 , 20 ] ( 10 , 20 ] ( 20 , 30 ] Levels: ( 10 , 20 ] ( 20 , 30 ] ( 30 , 40 ] ( 40 , 50 ] > table( cut( mtcars$ mpg, c ( seq( 10 , 50 , 10 ) ) ) ) ( 10 , 20 ] ( 20 , 30 ] ( 30 , 40 ] ( 40 , 50 ] 18 10 4 0 > prop.table( table( cut( mtcars$ mpg, c ( seq( 10 , 50 , 10 ) ) ) ) ) ( 10 , 20 ] ( 20 , 30 ] ( 30 , 40 ] ( 40 , 50 ] 0.5625 0.3125 0.1250 0.0000
也可以对二维数据表进行描述,比如给table函数输入两个因子,就可以计算二维的列联表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Arthritis ID Treatment Sex Age Improved 1 57 Treated Male 27 Some2 46 Treated Male 29 None3 77 Treated Male 30 None... 82 15 Placebo Female 66 Some83 71 Placebo Female 68 Some84 1 Placebo Female 74 Marked> table( Arthritis$ Treatment, Arthritis$ Improved) None Some Marked Placebo 29 7 7 Treated 13 7 21 > with( data = Arthritis, { table( Treatment, Improved) } ) Improved Treatment None Some Marked Placebo 29 7 7 Treated 13 7 21
如果变量太多,可以用with先加载数据。
处理列联表还可以使用xtabs函数
1 2 3 4 5 > xtabs( ~ Treatment+ Improved, data = Arthritis) Improved Treatment None Some Marked Placebo 29 7 7 Treated 13 7 21
~位置可以是公式,也可以省略。
margin.table函数可以单独根据一行或一列进行频数统计。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 > x <- xtabs( ~ Treatment+ Improved, data = Arthritis) > x Improved Treatment None Some Marked Placebo 29 7 7 Treated 13 7 21 > margin.table( x) [ 1 ] 84 > margin.table( x, 1 ) Treatment Placebo Treated 43 41 > margin.table( x, 2 ) Improved None Some Marked 42 14 28 > prop.table( x, 1 ) Improved Treatment None Some Marked Placebo 0.6744186 0.1627907 0.1627907 Treated 0.3170732 0.1707317 0.5121951 > addmargins( x) Improved Treatment None Some Marked Sum Placebo 29 7 7 43 Treated 13 7 21 41 Sum 42 14 28 84 > addmargins( x, 1 ) Improved Treatment None Some Marked Placebo 29 7 7 Treated 13 7 21 Sum 42 14 28 > addmargins( x, 2 ) Improved Treatment None Some Marked Sum Placebo 29 7 7 43 Treated 13 7 21 41
也可以进行三维列联表统计:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > y <- xtabs( ~ Treatment+ Improved+ Sex, data = Arthritis) > y, , Sex = Female Improved Treatment None Some Marked Placebo 19 7 6 Treated 6 5 16 , , Sex = Male Improved Treatment None Some Marked Placebo 10 0 1 Treated 7 2 5 > ftable( y) Sex Female Male Treatment Improved Placebo None 19 10 Some 7 0 Marked 6 1 Treated None 6 7 Some 5 2 Marked 16 5
5.5 独立性检验函数
独立性检验是根据频数信息判断两类因子彼此相关或相互独立的假设检验。所谓独立性就是指变量之间是独立的,没有关系。
三种独立性检验方法:
卡方检验
Fisher检验
Cochran-Mantel-Haenszel检验
假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。
原假设—没有发生;
备择假设—发生了;
具体作法是:根据问题的需要对所研究的总体作某种假设,记作H0;选取合适的统计量,这个统计量的选取要使得在假设H0成立时,其分布为已知;由实测的样本,计算出统计量的值,并根据预先给定的显著性水平进行检验,作出拒绝或接受假设H0的判断。
p-value就是Probability的值,它是一个通过计算得到的概率值,也就是在原假设为真时,得到最大的或者超出所得到的检验统计量值的概率。
一般将p值定位到0.05,当p<0.05拒绝原假设,p>0.05,不拒绝原假设。如果数据噪音比较大,可以放松限制条件,将p值设定为0.1,如果数据比较精确,可以设定为0.01。
vcd包中的chisq.test函数可以进行卡方独立检验:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 > mytable <- table( Arthritis$ Treatment, Arthritis$ Improved) > chisq.test( mytable) Pearson's Chi-squared test data: mytable X-squared = 13.055, df = 2, p-value = 0.001463 > mytable <- table(Arthritis$Sex,Arthritis$Improved) > chisq.test(mytable) Pearson' s Chi- squared testdata: mytable X- squared = 4.8407 , df = 2 , p- value = 0.08889 Warning message: In chisq.test( mytable) : Chi- squared近似算法有可能不准 > mytable <- table( Arthritis$ Improved, Arthritis$ Sex) > chisq.test( mytable) Pearson's Chi-squared test data: mytable X-squared = 4.8407, df = 2, p-value = 0.08889 Warning message: In chisq.test(mytable) : Chi-squared近似算法有可能不准
通过Fisher检验:
1 2 3 4 5 6 7 8 > mytable <- xtabs( ~ Treatment+ Improved, data= Arthritis) > fisher.test( mytable) Fisher's Exact Test for Count Data data: mytable p-value = 0.001393 alternative hypothesis: two.sided
p值都小于0.05说明变量不独立。
Cochran-Mantel-Haenszel检验:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > mytable <- xtabs( ~ Treatment+ Improved+ Sex, data= Arthritis) > mytable, , Sex = Female Improved Treatment None Some Marked Placebo 19 7 6 Treated 6 5 16 , , Sex = Male Improved Treatment None Some Marked Placebo 10 0 1 Treated 7 2 5 > mantelhaen.test( mytable) Cochran- Mantel- Haenszel test data: mytable Cochran- Mantel- Haenszel M^ 2 = 14.632 , df = 2 , p- value = 0.0006647
Treatment、Sex和Improved参数的先后位置很重要,比如下面的这个示例对比上面的示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 > mytable <- xtabs( ~ Treatment+ Sex+ Improved, data= Arthritis) > mytable, , Improved = None Sex Treatment Female Male Placebo 19 10 Treated 6 7 , , Improved = Some Sex Treatment Female Male Placebo 7 0 Treated 5 2 , , Improved = Marked Sex Treatment Female Male Placebo 6 1 Treated 16 5 > mantelhaen.test( mytable) Mantel- Haenszel chi- squared test with continuity correction data: mytable Mantel- Haenszel X- squared = 2.0863 , df = 1 , p- value = 0.1486 alternative hypothesis: true common odds ratio is not equal to 1 95 percent confidence interval: 0.8566711 8.0070521 sample estimates: common odds ratio 2.619048
5.6 相关性分析函数
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。简单来说就是变量之间是否有关系。
相关性衡量指标:
Pearson相关系数
Spearman相关系数
Kendall相关系数
偏相关系数
多分格(polychoric)相关系数
多系列(polyserial)相关系数
相关性中每种方法都没有独立的函数,均使用同一个函数cor。cor可以计算三种相关系数,包括Pearson、Spearman和Kendall,具体使用哪种算法可以通过method参数指定,默认使用Pearson系数。其他的相关系数:偏相关系数、多分格相关系数、多系列相关系数可以通过R的相关拓展包实现。比如ggm包中的pcor可以用来计算偏相关系数。
cor函数中的use参数表示如何对待缺失值,是不处理还是删除,可选的选项有"everything", “all.obs”, “complete.obs”, “na.or.complete”, 或 “pairwise.complete.obs”。
1 2 3 4 5 6 7 8 9 10 > cor( state.x77) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Population 1.00000000 0.2082276 0.10762237 - 0.06805195 0.3436428 - 0.09848975 - 0.3321525 0.02254384 Income 0.20822756 1.0000000 - 0.43707519 0.34025534 - 0.2300776 0.61993232 0.2262822 0.36331544 Illiteracy 0.10762237 - 0.4370752 1.00000000 - 0.58847793 0.7029752 - 0.65718861 - 0.6719470 0.07726113 Life Exp - 0.06805195 0.3402553 - 0.58847793 1.00000000 - 0.7808458 0.58221620 0.2620680 - 0.10733194 Murder 0.34364275 - 0.2300776 0.70297520 - 0.78084575 1.0000000 - 0.48797102 - 0.5388834 0.22839021 HS Grad - 0.09848975 0.6199323 - 0.65718861 0.58221620 - 0.4879710 1.00000000 0.3667797 0.33354187 Frost - 0.33215245 0.2262822 - 0.67194697 0.26206801 - 0.5388834 0.36677970 1.0000000 0.05922910 Area 0.02254384 0.3633154 0.07726113 - 0.10733194 0.2283902 0.33354187 0.0592291 1.00000000
这是对角矩阵,对角位置的数值为1,说明自己和自己的相关性为1,一般相关系数在0到1之间,正负号为正相关和负相关。
cov可以用来计算协方差,协方差可以用来计算两个变量的总体误差。在计算偏方差时需要用到协方差的结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > cov( state.x77) Population Income Illiteracy Life Exp Murder HS Grad Frost Population 19931683.7588 571229.7796 292.8679592 - 4.078425e+02 5663.523714 - 3551.509551 - 77081.97265 Income 571229.7796 377573.3061 - 163.7020408 2.806632e+02 - 521.894286 3076.768980 7227.60408 Illiteracy 292.8680 - 163.7020 0.3715306 - 4.815122e-01 1.581776 - 3.235469 - 21.29000 Life Exp - 407.8425 280.6632 - 0.4815122 1.802020e+00 - 3.869480 6.312685 18.28678 Murder 5663.5237 - 521.8943 1.5817755 - 3.869480e+00 13.627465 - 14.549616 - 103.40600 HS Grad - 3551.5096 3076.7690 - 3.2354694 6.312685e+00 - 14.549616 65.237894 153.99216 Frost - 77081.9727 7227.6041 - 21.2900000 1.828678e+01 - 103.406000 153.992163 2702.00857 Area 8587916.9494 19049013.7510 4018.3371429 - 1.229410e+04 71940.429959 229873.192816 262703.89306 Area Population 8.587917e+06 Income 1.904901e+07 Illiteracy 4.018337e+03 Life Exp - 1.229410e+04 Murder 7.194043e+04 HS Grad 2.298732e+05 Frost 2.627039e+05 Area 7.280748e+09
如果想计算一组变量和另一组变量之间的关系,而不是所有变量两两之间的关系。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > x <- state.x77[ , c ( 1 , 2 , 3 , 6 ) ] > y <- state.x77[ , c ( 4 , 5 ) ] > head( x) Population Income Illiteracy HS Grad Alabama 3615 3624 2.1 41.3 Alaska 365 6315 1.5 66.7 Arizona 2212 4530 1.8 58.1 Arkansas 2110 3378 1.9 39.9 California 21198 5114 1.1 62.6 Colorado 2541 4884 0.7 63.9 > head( y) Life Exp Murder Alabama 69.05 15.1 Alaska 69.31 11.3 Arizona 70.55 7.8 Arkansas 70.66 10.1 California 71.71 10.3 Colorado 72.06 6.8 > cor( x, y) Life Exp Murder Population - 0.06805195 0.3436428 Income 0.34025534 - 0.2300776 Illiteracy - 0.58847793 0.7029752 HS Grad 0.58221620 - 0.4879710
ggm包中pcor函数用来计算偏相关系数:
1 2 > pcor( c ( 1 , 2 , 3 , 5 , 6 ) , cov( state.x77) ) [ 1 ] 0.3132774
pcor(u, S)说明pcor需要两个重要参数,第一个参数是数值向量,前两个数值为要计算相关系数的下标,其余的数值为条件变量的下标,第二个参数为计算出来的协方差结果。
5.7 相关性检验函数
即使通过cor计算出很高的相关系数,仍然需要进行相关性检验
相关性检验用相关性检验函数cor.test,cor.test函数中alternative可以选择"two.sided", “less”, "greater"分别表示正负相关性、负相关和正相关,method可以选择哪种相关性分析方法。cor.test每次只能检测一组变量,使用起来麻烦一点。
1 2 3 4 cor.test( x, y, alternative = c ( "two.sided" , "less" , "greater" ) , method = c ( "pearson" , "kendall" , "spearman" ) , exact = NULL , conf.level = 0.95 , continuity = FALSE , ...)
1 2 3 4 5 6 7 8 9 10 11 12 > cor.test( state.x77[ , 3 ] , state.x77[ , 5 ] ) Pearson's product-moment correlation data: state.x77[, 3] and state.x77[, 5] t = 6.8479, df = 48, p-value = 1.258e-08 # p-value的值远小于0.05 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: 0.5279280 0.8207295 sample estimates: cor 0.7029752
可以看出p-value的值远小于0.05,所以拒绝了原假设(即两个变量之间无关)
置信区间:confidence interval,是指由样本统计量所构成的总体参数的估计区间。在统计学中,一个概率样本的置信区间是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的是被测量参数的测量指的可信程度。
示例:如果在一次大选中某人的支持率为55%,而置信水平0.95以上的置信区间是(50%,60%),那么他的真实支持率有百分之九十五的机率,落在百分之五十和百分之六十之间,因此他的真实支持率不足一半的可能性小于百分之5。
在psych包中corr.test函数可以进行多个变量之间的计算,也可以进行递归处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 > corr.test( state.x77) Call: corr.test( x = state.x77) Correlation matrix Population Income Illiteracy Life Exp Murder HS Grad Frost Area Population 1.00 0.21 0.11 - 0.07 0.34 - 0.10 - 0.33 0.02 Income 0.21 1.00 - 0.44 0.34 - 0.23 0.62 0.23 0.36 Illiteracy 0.11 - 0.44 1.00 - 0.59 0.70 - 0.66 - 0.67 0.08 Life Exp - 0.07 0.34 - 0.59 1.00 - 0.78 0.58 0.26 - 0.11 Murder 0.34 - 0.23 0.70 - 0.78 1.00 - 0.49 - 0.54 0.23 HS Grad - 0.10 0.62 - 0.66 0.58 - 0.49 1.00 0.37 0.33 Frost - 0.33 0.23 - 0.67 0.26 - 0.54 0.37 1.00 0.06 Area 0.02 0.36 0.08 - 0.11 0.23 0.33 0.06 1.00 Sample Size [ 1 ] 50 Probability values ( Entries above the diagonal are adjusted for multiple tests.) Population Income Illiteracy Life Exp Murder HS Grad Frost Area Population 0.00 1.00 1.00 1.00 0.23 1.00 0.25 1.00 Income 0.15 0.00 0.03 0.23 1.00 0.00 1.00 0.16 Illiteracy 0.46 0.00 0.00 0.00 0.00 0.00 0.00 1.00 Life Exp 0.64 0.02 0.00 0.00 0.00 0.00 0.79 1.00 Murder 0.01 0.11 0.00 0.00 0.00 0.01 0.00 1.00 HS Grad 0.50 0.00 0.00 0.00 0.00 0.00 0.16 0.25 Frost 0.02 0.11 0.00 0.07 0.00 0.01 0.00 1.00 Area 0.88 0.01 0.59 0.46 0.11 0.02 0.68 0.00 To see confidence intervals of the correlations, print with the short= FALSE option
如果想进行偏相关的检验,可以通过ggm包中的pcor.test函数进行相关检验:
1 2 3 4 5 6 7 8 9 10 11 12 > x <- pcor( c ( 1 , 2 , 3 , 5 , 6 ) , cov( state.x77) ) > x[ 1 ] 0.3132774 > pcor.test( x, 3 , 50 ) $ tval[ 1 ] 2.212924 $ df[ 1 ] 45 $ pvalue[ 1 ] 0.03201783
x为偏相关计算的相关系数,3为返回的变量数,50为样本数
返回三个值:t检验、自由度和p-value
t检验是用t分布理论推论差异发生的概率,从而比较两个平均数的差异是否显著,主要用于样本量小,一般小于30个,总体标准差未知的标准正态分布数据。
UScrime数据集为美国47个州的犯罪制度对犯罪率的影响信息。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 > UScrime M So Ed Po1 Po2 LF M.F Pop NW U1 U2 GDP Ineq Prob Time y 1 151 1 91 58 56 510 950 33 301 108 41 394 261 0.084602 26.2011 791 2 143 0 113 103 95 583 1012 13 102 96 36 557 194 0.029599 25.2999 1635 3 142 1 89 45 44 533 969 18 219 94 33 318 250 0.083401 24.3006 578 4 136 0 121 149 141 577 994 157 80 102 39 673 167 0.015801 29.9012 1969 5 141 0 121 109 101 591 985 18 30 91 20 578 174 0.041399 21.2998 1234 6 121 0 110 118 115 547 964 25 44 84 29 689 126 0.034201 20.9995 682 7 127 1 111 82 79 519 982 4 139 97 38 620 168 0.042100 20.6993 963 8 131 1 109 115 109 542 969 50 179 79 35 472 206 0.040099 24.5988 1555 9 157 1 90 65 62 553 955 39 286 81 28 421 239 0.071697 29.4001 856 10 140 0 118 71 68 632 1029 7 15 100 24 526 174 0.044498 19.5994 705 11 124 0 105 121 116 580 966 101 106 77 35 657 170 0.016201 41.6000 1674 12 134 0 108 75 71 595 972 47 59 83 31 580 172 0.031201 34.2984 849 13 128 0 113 67 60 624 972 28 10 77 25 507 206 0.045302 36.2993 511 14 135 0 117 62 61 595 986 22 46 77 27 529 190 0.053200 21.5010 664 15 152 1 87 57 53 530 986 30 72 92 43 405 264 0.069100 22.7008 798 16 142 1 88 81 77 497 956 33 321 116 47 427 247 0.052099 26.0991 946 17 143 0 110 66 63 537 977 10 6 114 35 487 166 0.076299 19.1002 539 18 135 1 104 123 115 537 978 31 170 89 34 631 165 0.119804 18.1996 929 19 130 0 116 128 128 536 934 51 24 78 34 627 135 0.019099 24.9008 750 20 125 0 108 113 105 567 985 78 94 130 58 626 166 0.034801 26.4010 1225 21 126 0 108 74 67 602 984 34 12 102 33 557 195 0.022800 37.5998 742 22 157 1 89 47 44 512 962 22 423 97 34 288 276 0.089502 37.0994 439 23 132 0 96 87 83 564 953 43 92 83 32 513 227 0.030700 25.1989 1216 24 131 0 116 78 73 574 1038 7 36 142 42 540 176 0.041598 17.6000 968 25 130 0 116 63 57 641 984 14 26 70 21 486 196 0.069197 21.9003 523 26 131 0 121 160 143 631 1071 3 77 102 41 674 152 0.041698 22.1005 1993 27 135 0 109 69 71 540 965 6 4 80 22 564 139 0.036099 28.4999 342 28 152 0 112 82 76 571 1018 10 79 103 28 537 215 0.038201 25.8006 1216 29 119 0 107 166 157 521 938 168 89 92 36 637 154 0.023400 36.7009 1043 30 166 1 89 58 54 521 973 46 254 72 26 396 237 0.075298 28.3011 696 31 140 0 93 55 54 535 1045 6 20 135 40 453 200 0.041999 21.7998 373 32 125 0 109 90 81 586 964 97 82 105 43 617 163 0.042698 30.9014 754 33 147 1 104 63 64 560 972 23 95 76 24 462 233 0.049499 25.5005 1072 34 126 0 118 97 97 542 990 18 21 102 35 589 166 0.040799 21.6997 923 35 123 0 102 97 87 526 948 113 76 124 50 572 158 0.020700 37.4011 653 36 150 0 100 109 98 531 964 9 24 87 38 559 153 0.006900 44.0004 1272 37 177 1 87 58 56 638 974 24 349 76 28 382 254 0.045198 31.6995 831 38 133 0 104 51 47 599 1024 7 40 99 27 425 225 0.053998 16.6999 566 39 149 1 88 61 54 515 953 36 165 86 35 395 251 0.047099 27.3004 826 40 145 1 104 82 74 560 981 96 126 88 31 488 228 0.038801 29.3004 1151 41 148 0 122 72 66 601 998 9 19 84 20 590 144 0.025100 30.0001 880 42 141 0 109 56 54 523 968 4 2 107 37 489 170 0.088904 12.1996 542 43 162 1 99 75 70 522 996 40 208 73 27 496 224 0.054902 31.9989 823 44 136 0 121 95 96 574 1012 29 36 111 37 622 162 0.028100 30.0001 1030 45 139 1 88 46 41 480 968 19 49 135 53 457 249 0.056202 32.5996 455 46 126 0 104 106 97 599 989 40 24 78 25 593 171 0.046598 16.6999 508 47 130 0 121 90 91 623 1049 3 22 113 40 588 160 0.052802 16.0997 849 > t.test( Prob ~ So, data = UScrime) Welch Two Sample t- test data: Prob by So t = - 3.8954 , df = 24.925 , p- value = 0.0006506 alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0 95 percent confidence interval: - 0.03852569 - 0.01187439 sample estimates: mean in group 0 mean in group 1 0.03851265 0.06371269
t.test(y ~ x):其中y为数值型变量,x为二分型的变量
如果数据满足正态分布,可以使用方差分析,如果不满足正态分布,就需要使用非参数的方法。在相关性检验中常常会听到参数检验和非参数检验。
参数检验,Parametric tests,是在总体分布形式已知的情况下,对总体分布的参数如均值、方差等进行推断的方法。也就是数据分布已知比如满足正态分布。
非参数检验,称为Nonparametric tests,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验。
5.8 绘图函数
R语言四大绘图系统:
基础绘图系统
lattice包
ggplot2包
grid包
基础绘图包:graphics包
通过命令ls将graphics包所有的函数都列举出来。
1 > ls( "package:graphics" )
arrows函数用来绘制箭头,hist函数绘制直方图,stars函数是绘制晶状体,pie函数绘制饼图,polygon函数绘制多边形图。
R基础绘图系统:
高级绘图
高级绘图是一步到位,可以直接绘制出图。
低级绘图
低级绘图不能单独使用,必须再高级绘图产生图形的基础上,对图形进行调整,比如加一条线,加上标题文字等。
R绘图输入数据:
散点图:x和y两个坐标数据
直方图:因子
热力图:数据矩阵
…
plot函数进行绘图:
如图,如果只是一列向量,则为序列为横坐标,纵坐标为向量值。
1 > plot( women$ height, women$ weight)
如图,如果是两列向量,则反映两个向量之间的关系。
1 plot( as.factor( mtcars$ cyl) )
如果输入的是因子,绘制出来的是直方图。
1 > plot( as.factor( mtcars$ cyl) , mtcars$ carb)
如果一个是因子,一个是向量,则绘制出的是箱线图。
1 > plot( mtcars$ carb, as.factor( mtcars$ cyl) )
如果第一个是向量,第二个是因子,绘制的是散列图。
1 > plot( as.factor( mtcars$ carb) , as.factor( mtcars$ cyl) )
如果两个都是因子,输出的是脊柱图。
1 > plot( women$ height ~ women$ weight)
这里plot绘制的是二者的关系图。
实际上,plot函数的参数主要由par提供。不同于plot函数,par函数的参数除个别外一旦设定,除非再次更改或重启R,否则就会对后续所有的绘图命令起作用。
1 > plot( as.factor( mtcars$ cyl) , col= c ( "red" , "green" , "blue" ) )
在设置参数之前,可以使用以下代码保存绘图系统的默认参数:
1 2 opar <- par( no.readonly = TRUE )
设置参数前可以先查看当前的参数值:
1 2 par( "usr" ) par( c ( "usr" , "fin" ) )
大部分参数既可以在par中设置,又可以在plot中设置,区别在于前者设置的参数对全局起作用,后者设置的参数只对本条命令起作用,相当于plot中的...参数,个别参数在两种情况下面对的对象也不同。还有,以下参数只能在par中使用:
ask
fig, fin
lheight
mai, mar, mex, mfcol, mfrow, mfg
new
oma, omd, omi
pin, plt, ps, pty
usr
xlog, ylog
ylbias
5.9 自定义函数
直接在终端中输入函数名,会给出源代码:
R自定义函数:
函数名称:函数命令与功能相关,可以是字母和数字的组合,但必须是字母开头
函数声明
函数参数
函数体
利用function函数来声明
1 2 3 myfun <- function ( 选项参数) { 函数体 }
示例:计算偏度与峰度的函数
偏度(skewness)是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。
峰度(peakedness; kurtosis)又称峰态系数。表征概率密度分布曲线在平均值处峰值的特征数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > mystats( x) n mean stdev skew kurtosis 87.000000 440.000000 252.586619 - 5.285971 - 12.208086 > mystats <- function ( x, na.omit= FALSE ) { + if ( na.omit) + x <- x[ ! is.na ( x) ] + m <- mean( x) + n <- length ( x) + s <- sd( x) + skew <- sum ( ( x- m) ^ 3 / s^ 3 ) / n+ kurt <- sum ( ( x- m) ^ 4 / s^ 4 ) / n- 3 + return ( c ( n= n, mean= m, stdev= s, skew= skew, kurtosis= kurt) ) + } > mystats( x) n mean stdev skew kurtosis 87.000000 440.000000 252.586619 0.000000 - 1.241451
循环和向量化操作:
函数内部通过循环实现向量化操作。
循环三部分:
for循环:
1 2 3 4 5 6 7 8 9 10 11 > for ( i in 1 : 10 ) { print ( "Hello,World" ) } [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World"
while循环:
1 2 3 4 5 6 7 8 9 10 11 > i= 1 ;while ( i <= 10 ) { print ( "Hello,World" ) ;i= i+ 1 ;} [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World" [ 1 ] "Hello,World"
if…else…:
1 2 3 4 5 > score= 70 ;if ( score > 60 ) { print ( "Passwd" ) } else { print ( "Failed" ) } [ 1 ] "Passwd" > ifelse( score > 60 , print ( "Passwd" ) , print ( "Failed" ) ) [ 1 ] "Passwd" [ 1 ] "Passwd"
也可以使用switch。
6 数据分析实战
6.1 线性回归一
回归regression,通常指那些用一个或多个预测变量,也称自变量或解释变量,来预测相应变量,也称为因变量、校标变量或结果变量的方法。
普通最小二乘回归法(OLS)
Y ^ i = β ^ 0 + β ^ 1 X 1 i + ⋯ + β ^ k X k i i = 1 ⋯ n \hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1X_{1i}+\cdots +\hat{\beta}_kX_{ki}\quad \quad i=1\cdots n
Y ^ i = β ^ 0 + β ^ 1 X 1 i + ⋯ + β ^ k X ki i = 1 ⋯ n
Y ^ i \hat{Y}_i Y ^ i i i i Y Y Y
X i j X_{ij} X ij i i i j j j
β ^ 0 \hat{\beta}_0 β ^ 0 0 0 0 Y Y Y
β ^ j \hat{\beta}_j β ^ j j j j X j X_j X j Y Y Y
满足OLS模型统计假设 :
正态性:对于固定的自变量值,因变量值成正态分布。
独立性:因变量之间相互独立。
线性:因变量与自变量之间为线性相关。
同方差性:因变量的方差不随自变量的水平不同而变化。也可称作不变方差。
==注意==:只有满足以上条件才能运用lm函数进行拟合。
可是使用lm函数进行线性回归模型分析:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 > fit <- lm( weight ~ height, data = women) > fitCall: lm( formula = weight ~ height, data = women) Coefficients: ( Intercept) height - 87.52 3.45 > summary( fit) Call: lm( formula = weight ~ height, data = women) Residuals: Min 1 Q Median 3 Q Max - 1.7333 - 1.1333 - 0.3833 0.7417 3.1167 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) - 87.51667 5.93694 - 14.74 1.71e-09 * * * height 3.45000 0.09114 37.85 1.09e-14 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.525 on 13 degrees of freedom Multiple R- squared: 0.991 , Adjusted R- squared: 0.9903 F - statistic: 1433 on 1 and 13 DF, p- value: 1.091e-14 > summary.lm( fit) Call: lm( formula = weight ~ height, data = women) Residuals: Min 1 Q Median 3 Q Max - 1.7333 - 1.1333 - 0.3833 0.7417 3.1167 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) - 87.51667 5.93694 - 14.74 1.71e-09 * * * height 3.45000 0.09114 37.85 1.09e-14 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.525 on 13 degrees of freedom Multiple R- squared: 0.991 , Adjusted R- squared: 0.9903 F - statistic: 1433 on 1 and 13 DF, p- value: 1.091e-14
使用summary和使用summary.lm结果相同,因为使用summary,会自动调用其子函数summary.lm。
Call列出使用的回归公式;
Residuals为残差,真实值和预测值之间的差,残差值越小说明模型越精确。
Coefficients为系数项,Intercept为截距,即x为0时,y轴的坐标。
因此公式为:weight = 3.45000×Height-87.51667
Pr即p-value,估计系数为0假设的概率,小于0.05比较好
R对p值和t值进行了标记,分为五个等级,***结果最好。
Residual standard error: 1.525 on 13 degrees of freedom为残差标准误差,误差越小越好。
Multiple R-squared为R方判定系数,衡量模型拟合质量的指标,取值在0和1之间,值越大越好,它是表示回归模型所能解释的响应变量的方差比例,即这个模型能够解释99.1%的数据,只有0.9%的数据不符合此模型。
F-statistic为F统计量,这个值说明模型是否显著,也是用p-value来衡量,p-value值越小越好,说明模型越显著。
==重点==:一般首先看F统计量,如果不小于0.05,这个模型没有价值,需要重新进行拟合,如果小于0.05再看R方,看模型能够解释多少变量。
6.2 线性回归二
除了summary可以查看运行结果,还可以通过其他函数进行查看:
函数:
summary:展示拟合模型的详细结果
coefficients:列出拟合模型的模型参数(截距项和斜率),
confint:提供模型参数的置信区间(默认95%)
fitted:列出拟合模型的预测值
residuals:列出拟合模型的残差值
anova:生成一个拟合模型的方差分析表,或者比较两个或更多拟合模型的方差分析表
vcov:列出模型参数的协方差矩阵
AIC:输出赤池信息统计量
plot:生成评价拟合模型的诊断图
predict:用拟合模型对新的数据集预测响应变量值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 > fit <- lm( weight ~ height, data = women) > fitCall: lm( formula = weight ~ height, data = women) Coefficients: ( Intercept) height - 87.52 3.45 > coefficients( fit) ( Intercept) height - 87.51667 3.45000 > confint( fit) 2.5 % 97.5 % ( Intercept) - 100.342655 - 74.690679 height 3.253112 3.646888 > confint( fit, level = 0.5 ) 25 % 75 % ( Intercept) - 91.635892 - 83.397441 height 3.386767 3.513233 > fitted( fit) 1 2 3 4 5 6 7 8 9 10 11 12 112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833 143.6333 147.0833 150.5333 13 14 15 153.9833 157.4333 160.8833 > women$ weight - fitted( fit) 1 2 3 4 5 6 7 8 9 2.41666667 0.96666667 0.51666667 0.06666667 - 0.38333333 - 0.83333333 - 1.28333333 - 1.73333333 - 1.18333333 10 11 12 13 14 15 - 1.63333333 - 1.08333333 - 0.53333333 0.01666667 1.56666667 3.11666667 > residuals( fit) 1 2 3 4 5 6 7 8 9 2.41666667 0.96666667 0.51666667 0.06666667 - 0.38333333 - 0.83333333 - 1.28333333 - 1.73333333 - 1.18333333 10 11 12 13 14 15 - 1.63333333 - 1.08333333 - 0.53333333 0.01666667 1.56666667 3.11666667 > predict( fit, women) 1 2 3 4 5 6 7 8 9 10 11 12 112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833 143.6333 147.0833 150.5333 13 14 15 153.9833 157.4333 160.8833 > plot( fit) Hit < Return> to see next plot: Hit < Return> to see next plot: Hit < Return> to see next plot: Hit < Return> to see next plot:
通过abline函数生成拟合曲线:
1 2 > plot( women$ height, women$ weight) > abline( fit)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 > fit2 <- lm( weight ~ height+ I( height^ 2 ) , data= women) > fit2Call: lm( formula = weight ~ height + I( height^ 2 ) , data = women) Coefficients: ( Intercept) height I( height^ 2 ) 261.87818 - 7.34832 0.08306 > summary( fit2) Call: lm( formula = weight ~ height + I( height^ 2 ) , data = women) Residuals: Min 1 Q Median 3 Q Max - 0.50941 - 0.29611 - 0.00941 0.28615 0.59706 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) 261.87818 25.19677 10.393 2.36e-07 * * * height - 7.34832 0.77769 - 9.449 6.58e-07 * * * I( height^ 2 ) 0.08306 0.00598 13.891 9.32e-09 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.3841 on 12 degrees of freedom Multiple R- squared: 0.9995 , Adjusted R- squared: 0.9994 F - statistic: 1.139e+04 on 2 and 12 DF, p- value: < 2.2e-16 > plot( women$ height, women$ weight) > abline( fit) > lines( women$ height, fitted( fit2) , col= "red" )
注意:abline函数只能绘制直线,lines函数可以绘制曲线。在线性回归时,fit2 <- lm(weight ~ height+I(height^2),data=women)中的二次项,不能直接用height^2,因为倒三角符号^具有特殊的含义。
拟合多项式不是越多越好,多项式越多,可能存导致拟合。
6.3 多元线性回归
lm函数输入数据必须时数据框的格式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 > states <- as.data.frame( state.x77[ , c ( "Murder" , "Population" , "Illiteracy" , "Income" , "Frost" ) ] ) > states Murder Population Illiteracy Income Frost Alabama 15.1 3615 2.1 3624 20 Alaska 11.3 365 1.5 6315 152 Arizona 7.8 2212 1.8 4530 15 Arkansas 10.1 2110 1.9 3378 65 California 10.3 21198 1.1 5114 20 ... Virginia 9.5 4981 1.4 4701 85 Washington 4.3 3559 0.6 4864 32 West Virginia 6.7 1799 1.4 3617 100 Wisconsin 3.0 4589 0.7 4468 149 Wyoming 6.9 376 0.6 4566 173 > fit <- lm( Murder ~ Population+ Illiteracy+ Income+ Frost, data = states) > summary( fit) Call: lm( formula = Murder ~ Population + Illiteracy + Income + Frost, data = states) Residuals: Min 1 Q Median 3 Q Max - 4.7960 - 1.6495 - 0.0811 1.4815 7.6210 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) 1.235e+00 3.866e+00 0.319 0.7510 Population 2.237e-04 9.052e-05 2.471 0.0173 * Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 * * * Income 6.442e-05 6.837e-04 0.094 0.9253 Frost 5.813e-04 1.005e-02 0.058 0.9541 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.535 on 45 degrees of freedom Multiple R- squared: 0.567 , Adjusted R- squared: 0.5285 F - statistic: 14.73 on 4 and 45 DF, p- value: 9.133e-08 > coef( fit) ( Intercept) Population Illiteracy Income Frost 1.2345634112 0.0002236754 4.1428365903 0.0000644247 0.0005813055 > options( digits = 4 ) > coef( fit) ( Intercept) Population Illiteracy Income Frost 1.235e+00 2.237e-04 4.143e+00 6.442e-05 5.813e-04
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > fit <- lm( mpg ~ hp+ wt+ hp: wt, data = mtcars) > summary( fit) Call: lm( formula = mpg ~ hp + wt + hp: wt, data = mtcars) Residuals: Min 1 Q Median 3 Q Max - 3.063 - 1.649 - 0.736 1.421 4.551 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) 49.80842 3.60516 13.82 5.0e-14 * * * hp - 0.12010 0.02470 - 4.86 4.0e-05 * * * wt - 8.21662 1.26971 - 6.47 5.2e-07 * * * hp: wt 0.02785 0.00742 3.75 0.00081 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.15 on 28 degrees of freedom Multiple R- squared: 0.885 , Adjusted R- squared: 0.872 F - statistic: 71.7 on 3 and 28 DF, p- value: 2.98e-13
fit <- lm(mpg ~ hp+wt+hp:wt,data = mtcars)中hp:wt表示hp和wt之间是某种交互关系。
当存在多个变量,各个变量之间存在相互关系,是否需要添加交互项或者多项式来提高拟合度?对于这个问题,可以使用AIC函数来比较模型。
AIC全名为Akaike’s An Information Criterion
1 2 3 4 5 6 > fit1 <- lm( Murder ~ Population + Illiteracy + Income + Frost, data= states) > fit2 <- lm( Murder ~ Population + Illiteracy, data= states) > AIC( fit1, fit2) df AIC fit1 6 241.6 fit2 4 237.7
结果显示,fit2的拟合度最好
如果太多这样的情况,效果就不好了,可以采用逐步回归法和全子集回归法。
逐步回归法中模型会一次添加或删除一个变量,直到达到某个节点为止,继续添加或者删除变量,模型不再继续变化,如果每次增加变量,则向前逐步回归,如果每次删除变量,向后逐步回归。
全子集回归法是取所有可能的模型,然后从中计算最佳的模型。
全子集回归法要比逐步回归法要好,因为为检测到所有的模型,但是缺点是变量太多,会有大量的计算,会非常慢,这两种方法都需要通过R拓展包来实现。MASS包中的stepAIC函数可以进行逐步回归法的计算,leaps包中的regsubsets可以进行全子集回归法计算。
拟合效果最佳,而没有实际意义的模型是没有意义的,需要对数据有所了解。
6.4 回归诊断
满足OLS模型统计假设 :
正态性:对于固定的自变量值,因变量值成正态分布。
独立性:因变量之间相互独立。
线性:因变量与自变量之间为线性相关。
同方差性:因变量的方差不随自变量的水平不同而变化。也可称作不变方差。
==注意==:只有满足以上条件才能运用lm函数进行拟合。
1 2 3 4 5 6 7 8 9 10 11 12 > fit <- lm( weight ~ height, data = women) > fitCall: lm( formula = weight ~ height, data = women) Coefficients: ( Intercept) height - 87.52 3.45 > par( mfrow= c ( 2 , 2 ) ) > plot( fit)
通过plot(fit)可以绘制出四幅图,这四幅图就是反映上面的OLS模型的四个条件。
第一幅图反映残差和拟合是否为线性关系,图中的点为残差值的分布,曲线为拟合曲线。
第二幅图为QQ图,QQ图用来描述正态性,如果数据呈正态性,则为一条直线,图中残差值也为一条直线分布,说明满足正态性要求。
第三幅图为位置与尺寸图,用来描述同方差性,如果满足不变方差的假设,那么图中水平线附近的点应该是随机分布的,如图,也满足条件。
第四幅图为残差与杠杆图,提供了对单个数据值的观测,可以看出哪些点偏差较远,可以用来鉴别离群点、高杠杆点和强影响点。
离群点表示回归模型对这个点的预测效果不好,残差值比较大,不适合模型。
高杠杆点表示异常的预测变量的组合。
强影响点表示这个值对模型参数的估计产生的影响过大,可以用Cook’s distance来鉴别
对于这些异常点,因为会干扰到模型的拟合,如果将这些点删除掉,拟合的结果会更好,如果数据中这些点干扰太大,可以删除这些观察点重新进行拟合,或者对数据进行转换,比如对所有数据取指数、取对数等,来减少这些点的影响,但是对于这些数据的修改也会存在一定的争议,因为这些干扰的数据也是数据本身的一部分,也是客观存在的,如果删除或者转换就可能违背了客观事实,类似于实验中,为了试验数据好看,去掉不符合结论的样品。甚至先有结论,然后挑选符合结论的样品进行分析。
上述四幅图并没有反映独立性的,独立性没有办法通过图来进行分辨,只能从搜集的数据中验证。
给拟合函数添加二次项,进行拟合:
1 2 3 4 > fit2 <- lm( weight ~ height + I( height^ 2 ) , data= women) > opar <- ( no.readonly = TRUE ) > par( mfrow= c ( 2 , 2 ) ) > plot( fit2)
为了验证模型准确性,可以进行抽样法验证
数据集中有1000个样本,随机抽取500个数据进行回归分析;
模型建好之后,利用predict函数,对剩余500个样本进行预测,比较残差值;
如果预测准确,说明模型可以,否则就需要调整模型。
6.5 方差分析一
方差分析,称为Analysis of Variance,简称ANOVA,也称为"变异数分析”,用于两个及两个以上样本均数差别的显著性检验。从广义上来讲,方差分析也属于回归分析的一种。只不过线性回归的因变量一般是连续型变量。而当自变量是因子时,研究关注的重点通常会从预测转向不同组之间差异的比较。这就是方差分析。
R中因子的应用 :计算频数、独立性检验、相关性检验、方差分析、主成分分析、因子分析……
方差分析会大量用在科学研究中,例如实验设计时,进行分组比较,例如药物研究实验,处理组与对照组进行比较
方差分析分为多种:
单因素方差分析ANOVA(组内,组间)
双因素方差分析ANOVA
协方差分析ANCOVA
多元方差分析MANOVA
多元协方差分析MANCOVA
单因素组间方差分析
如图,对10位患有某种病的患者进行治疗,有两种治疗方案,将患者分为两组,每组采用不同的方案进行治疗。这里每种人数相同,为均衡分组,如果每组人数不同,则为非均衡分组。由于只有一种变量:治疗方案。因此为单因素组间方差分析。
单因素组内方差分析
如果验证CBT方案更好,现在修改治疗方案如下:
患者进行五周和六个月的治疗,这里时间不同,为组内因子,与前面的组间因子不同,这种方法称为单因素组内方差分析。实验中每位患者分别进行了两次治疗,也成为重复测量方差分析。
双因素方差分析
这种方案设计既有组间因子也有组内因子,即为多因素方差分析
协方差分析(ANCOVA)
如果方差分析中,包含了协变量,就属于协方差分析,ANCOVA。如果其他病对此疗法有影响,即试验中多了干扰变量,这种干扰变量也称为协变量,如果方差分析中包含了协变量,就属于协方差分析。
多元方差分析(MANOVA)
如果方差研究中包含了多个因变量,那么这种实验设计称为多元方差分析,简称为MANOVA。
多元协方差分析(MANCOVA)
如果多元方差分析中存在协变量,那么就称为多元协方差分析。
方差分析可以使用lm函数进行拟合,不过一般都使用aov函数进行分析,二者在格式上有差别,但是aov函数的使用和lm函数几乎是一致的。
1 aov( formula, data = NULL , projections = FALSE , qr = TRUE , contrasts = NULL , ...)
方差分析公式中特殊符号 :
各种方差分析公式写法 :
==注意==:在方差分析中自变量的顺序很重要,如果是平衡设计还好,如果是非平衡实验设计或者存在协变量值,变量的顺序影响比较大。
==顺序很重要!==
当自变量与其他自变量或者协变量相关时,没有明确的方法可以评价自变量对因变量的贡献。例如,含因子A、B和因变量y的双因素不平衡因子设计,有三种效应:A和B的主效应,A和B的交互效应。假设你正使用如下表达式对数据进行建模:
Y~A+B A:B
有三种类型的方法可以分解等式右边各效应对y所解释的方差。A:B交互项根据A和B调整。A:B交互项同时根据A和B调整。A:B做调整,A:B交互项根据A和B调整。
6.6 方差分析二
6.6.1 单因素方差分析
使用multcomp包中的cholesterol数据集(50名患者接受降低胆固醇药物的五种治疗方案的数据)来进行演示。五十个患者分成十人一组,每天服用20克药物。第一组一天一次性服用20克药物;第二组一天分两次服用20克药物;第三组一天分四次服用20克药物。剩余两组办法是drugD和drugE,为两种候选药物。里面只有治疗方案一个因子,所以是单因素方差分析。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 > cholesterol trt response 1 1 time 3.861 2 1 time 10.387 3 1 time 5.906 4 1 time 3.061 5 1 time 7.720 6 1 time 2.714 7 1 time 4.924 8 1 time 2.304 9 1 time 7.530 10 1 time 9.412 11 2 times 10.399 12 2 times 8.603 13 2 times 13.632 14 2 times 3.505 15 2 times 7.770 16 2 times 8.627 17 2 times 9.227 18 2 times 6.316 19 2 times 15.826 20 2 times 8.344 21 4 times 13.962 22 4 times 13.961 23 4 times 13.918 24 4 times 8.053 25 4 times 11.043 26 4 times 12.369 27 4 times 10.392 28 4 times 9.029 29 4 times 12.842 30 4 times 18.179 31 drugD 16.982 32 drugD 15.458 33 drugD 19.979 34 drugD 14.739 35 drugD 13.585 36 drugD 10.865 37 drugD 17.590 38 drugD 8.819 39 drugD 17.963 40 drugD 17.632 41 drugE 21.512 42 drugE 27.244 43 drugE 20.520 44 drugE 15.771 45 drugE 22.885 46 drugE 23.953 47 drugE 21.593 48 drugE 18.306 49 drugE 20.385 50 drugE 17.307 attach( cholesterol) > table( trt) trt 1 time 2 times 4 times drugD drugE 10 10 10 10 10 > aggregate( response, by= list ( trt) , FUN= mean) Group.1 x 1 1 time 5.782 2 2 times 9.225 3 4 times 12.375 4 drugD 15.361 5 drugE 20.948 > fit <- aov( response ~ trt, data= cholesterol) > fitCall: aov( formula = response ~ trt, data = cholesterol) Terms: trt Residuals Sum of Squares 1351.4 468.8 Deg. of Freedom 4 45 Residual standard error: 3.227 Estimated effects may be unbalanced > summary( fit) Df Sum Sq Mean Sq F value Pr( > F ) trt 4 1351 338 32.4 9.8e-13 * * * Residuals 45 469 10 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1
方差分析结果主要看F值和p值,F值越大说明组间差异越显著,这里就是五组之间平均值的差别,而p-value则是用来衡量F值,p值越小说明F值越可靠。这里可以看出p-value值非常小,说明F检测值非常显著,五组治疗方法效果不同。
同样可以使用plot绘制方差结果:
1 2 > par( mfrow= c ( 2 , 2 ) ) > plot( fit)
下面用lm函数进行方差分析:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 > fit.lm <- lm( response~ trt, data= cholesterol) > fit.lmCall: lm( formula = response ~ trt, data = cholesterol) Coefficients: ( Intercept) trt2times trt4times trtdrugD trtdrugE 5.78 3.44 6.59 9.58 15.17 > summary( fit.lm) Call: lm( formula = response ~ trt, data = cholesterol) Residuals: Min 1 Q Median 3 Q Max - 6.542 - 1.967 - 0.002 1.890 6.601 Coefficients: Estimate Std. Error t value Pr( > | t| ) ( Intercept) 5.78 1.02 5.67 9.8e-07 * * * trt2times 3.44 1.44 2.39 0.021 * trt4times 6.59 1.44 4.57 3.8e-05 * * * trtdrugD 9.58 1.44 6.64 3.5e-08 * * * trtdrugE 15.17 1.44 10.51 1.1e-13 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.23 on 45 degrees of freedom Multiple R- squared: 0.742 , Adjusted R- squared: 0.72 F - statistic: 32.4 on 4 and 45 DF, p- value: 9.82e-13
F检测值和p-value和aov函数都一样,所以lm函数也可以进行方差分析。
6.6.2 协方差分析
使用multcomp包中的litter数据集,litter数据集为怀孕小鼠的数据集。该实验不是均衡设计,每个小鼠接受不同剂量药物处理,分别是不处理(0)、5单位剂量、50单位剂量和500单位剂量,这是自变量,产下幼崽的体重均值为因变量。因为怀孕的总时间有差异,会影响到幼崽的体重,所以属于协变量,这是一个协方差的例子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > table( litter$ dose) 0 5 50 500 20 19 18 17 > attach( litter) > aggregate( weight, by = list ( dose) , FUN= mean) Group.1 x 1 0 32.31 2 5 29.31 3 50 29.87 4 500 29.65 > fit <- aov( weight ~ gesttime+ dose, data= litter) > summary( fit) Df Sum Sq Mean Sq F value Pr( > F ) gesttime 1 134 134.3 8.05 0.006 * * dose 3 137 45.7 2.74 0.050 * Residuals 69 1151 16.7 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1
F值表明,怀孕时间和小鼠出生体重相关;控制怀孕时间,药物剂量和出生体重相关。证明药物是有影响的,而不是随机性产生的。
6.6.3 双因素方差分析
下面看一个双因素方差分析案例:
使用ToothGrowth数据集,这个数据集是200只豚鼠分别用两种喂食方法,橙汁(包含维生素C,也包含其他维生素)和维生素C,每种喂食方法中,抗坏血栓含量有三个水平,分别是0.5mg、1mg、2mg。每组分别选择10只豚鼠做实验,刚好60只,最后测试牙齿长度,看哪种更有利于牙齿生长。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 > ToothGrowth len supp dose 1 4.2 VC 0.5 2 11.5 VC 0.5 3 7.3 VC 0.5 4 5.8 VC 0.5 5 6.4 VC 0.5 ... 56 30.9 OJ 2.0 57 26.4 OJ 2.0 58 27.3 OJ 2.0 59 29.4 OJ 2.0 60 23.0 OJ 2.0 > attach( ToothGrowth) The following object is masked from litter: dose > xtabs( ~ supp+ dose) dose supp 0.5 1 2 OJ 10 10 10 VC 10 10 10 > aggregate( len, by= list ( supp, dose) , FUN= mean) Group.1 Group.2 x 1 OJ 0.5 13.23 2 VC 0.5 7.98 3 OJ 1.0 22.70 4 VC 1.0 16.77 5 OJ 2.0 26.06 6 VC 2.0 26.14 > aggregate( len, by= list ( supp, dose) , FUN= sd) Group.1 Group.2 x 1 OJ 0.5 4.460 2 VC 0.5 2.747 3 OJ 1.0 3.911 4 VC 1.0 2.515 5 OJ 2.0 2.655 6 VC 2.0 4.798 > class ( ToothGrowth$ dose) [ 1 ] "numeric" > ToothGrowth$ dose <- factor( dose) > class ( ToothGrowth$ dose) [ 1 ] "factor" > fit <- aov( len ~ supp* dose, data= ToothGrowth) > summary( fit) Df Sum Sq Mean Sq F value Pr( > F ) supp 1 205 205 15.57 0.00023 * * * dose 2 2426 1213 92.00 < 2e-16 * * * supp: dose 2 108 54 4.11 0.02186 * Residuals 54 712 13 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1
fit <- aov(len ~ supp*dose,data=ToothGrowth)代码中是*号,这里是两个变量的方差分析,两个变量之间还有交互,所以应该写成乘号,等价于:fit <- aov(len ~ supp+dose+supp:dose,data=ToothGrowth)。
supp和dose结果表明不同的喂食方法和剂量对豚鼠牙齿生长都有影响。
使用HH包中的interaction.plot函数可以对结果进行可视化:
1 2 3 > interaction.plot( dose, supp, len, type= "b" , + col= c ( "red" , "blue" ) , pch= c ( 16 , 18 ) , + main = "Interaction between Dose and Supplement Type" )
6.6.4 多元方差分析
使用UScereal数据集,这里研究的是美国谷物中的卡路里、脂肪和糖类含量是否会因为储物架的不同而发生变化。其中shelf列1代表低货架,2代表中货架,3代表顶层货架,其中卡路里、脂肪和糖类含量的变化是因变量,货架水平是自变量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 > attach( UScereal) > shelf <- factor( shelf) > aggregate( cbind( calories, fat, sugars) , by= list ( shelf) , FUN= mean) Group.1 calories fat sugars 1 1 119.5 0.6621 6.295 2 2 129.8 1.3413 12.508 3 3 180.1 1.9449 10.857 > fit <- manova( cbind( calories, fat, sugars) ~ shelf) > summary( fit) Df Pillai approx F num Df den Df Pr( > F ) shelf 2 0.402 5.12 6 122 1e-04 * * * Residuals 62 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 > summary.aov( fit) Response calories : Df Sum Sq Mean Sq F value Pr( > F ) shelf 2 50435 25218 7.86 0.00091 * * * Residuals 62 198860 3207 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Response fat : Df Sum Sq Mean Sq F value Pr( > F ) shelf 2 18.4 9.22 3.68 0.031 * Residuals 62 155.2 2.50 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 Response sugars : Df Sum Sq Mean Sq F value Pr( > F ) shelf 2 381 191 6.58 0.0026 * * Residuals 62 1798 29 - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1
因为已经因变量有多个,不能通过+将其合并,需要通过cbind将其合并成数据框,也可以使用summary.aov分别查看每个变量的结果。通过检测结果可以发现,三组中每组营养成分的测量值是不同的,差异结果显著。
注意:aggregate只能接受一个数据,可以通过cbind将三个变量组成一个数据框。
6.7 功效分析
功效分析,power analysis,可以帮助在给定置信度的情况下,判断检测到给定效应值时所需的样本量。反过来,它也可以在给定置信度水平情况下,计算在某样本量内能检测到给定效应值的概率。
功效分析函数 :pwr包中的函数
函数
功效计算的对象
pwr.2p.test()两比例(n相等)
pwr.2p2n.test()两比例(n不相等)
pwr.anova.test()平衡的单因素ANOVA
pwr.chisq.test()卡方检验
pwr.f2.test()广义线性模型
pwr.p.test()比例(单样本)
pwr.r.test()相关系数
pwr.t.test()t检验(单样本、两样本、配对)
pwr.t2n.test()t检验(n不相等的两样本)
功效分析的理论基础:
样本大小指的是实验设计中每种条件/组中观测的数目。
显著性水平(也称为alpha)由Ⅰ型错误的概率来定义。也可以把它看做是发现效应不发生的概率。
功效通过Ⅰ减去Ⅱ型错误的概率来定义。我们可以把它看做是真实效应发生的概率。
效应值指的是在备择或研究假设下效应的量。效应值的表达式依赖于假设检验中使用的统计方法。
案例:老板的领导风格对员工满意度的影响,是否超过薪水和工作小费对员工满意度的影响,领导风格可以用四个变量来估计,薪水和小费与三个变量有关,过去的经验表明,薪水和小费能够解决30%员工满意度的方差,而从现实出发,领导风格至少能解释35%的方差,假定显著性水平为0.05,那么在95%的置信度情况下,需要多少受试者才能得到这样的方差贡献率。
线性回归的功效分析可以使用pwr包中的pwr.f2.test函数进行计算,其中sig.level表示显著性水平,power为功效水平,u和v分别为分子自由度和分母自由度,f2为效应值。
pwr.f2.test函数使用如下:
1 pwr.f2.test( u = NULL , v = NULL , f2 = NULL , sig.level = 0.05 , power = NULL )
上面的案例分析如下,其中f2的值根据公式计算出来。
1 2 3 4 5 6 7 8 9 > pwr.f2.test( u= 3 , sig.level = 0.05 , power= 0.9 , f2= 0.0769 ) Multiple regression power calculation u = 3 v = 184.2 f2 = 0.0769 sig.level = 0.05 power = 0.9
可以得到v为184.2,假设显著性水平为0.05,在90%的置信度的情况下,至少需要185个受试者才可以。
假设两组样品做单因素方差分析,要达到0.9的功效,效应值为0.25,并选择0.05的显著性水平,那么每组需要多少样本量?
可以使用pwr.anova.test()函数对平衡单因素方差进行功效分析:
1 pwr.anova.test( k = NULL , n = NULL , f = NULL , sig.level = 0.05 , power = NULL )
其中k为组的个数,这里为两组;n为各组的样本大小,即要求的量,f是效应值,sig.level为显著性水平,power为功效水平。
1 2 3 4 5 6 7 8 9 10 11 > pwr.anova.test( k= 2 , f= 0.25 , sig.level = 0.05 , power = 0.9 ) Balanced one- way analysis of variance power calculation k = 2 n = 85.03 f = 0.25 sig.level = 0.05 power = 0.9 NOTE: n is number in each group
n为所求的值,可知n至少应为86,即每组中至少86个样本,由于是两组,所以总体样本数为其二倍,172个样本。
7 广义线性模型
线性回归和方差分析都是基于正态分布的假设。在线性模型中,可以通过一系列连续型或类别型预测变量来预测正态分布的响应变量,但是实际的数据分析中,呈简单线性分布的数据只占很少的一部分,绝大部分数据都是无规则分布的,通过数据分析来找到规律。刚开始假设数据为正态分布也不合理,例如二值型变量,比如多分类变量,结果变量也可能呈条件分布,对于这些数据不能用简单线性回归来处理,需要拓宽简单线性回归的方法,提出了广义线性回归。
线性回归和方差分析都是基于正态分布的假设,广义线性模型扩展了线性模型的框架,它包含了非正态因变量的分析。
在R中可以通过glm(Generalized Linear Models)函数进行广义线性回归分析。
1 2 3 4 glm( formula, family = gaussian, data, weights, subset, na.action, start = NULL , etastart, mustart, offset, control = list ( ...) , model = TRUE , method = "glm.fit" , x = FALSE , y = TRUE , singular.ok = TRUE , contrasts = NULL , ...)
这个函数与lm函数类似,其中最重要的参数为概率分布family,和相应的连接函数formula。
如果glm中family = gaussian,则结果和lm函数结果一致。
广义线性模型是通过拟合相应变量的条件均值的一个函数。假设响应变量服从指数分布族中的某个分布,并不仅限于正态分布,这样极大扩展了标准线性模型,模型参数估计的推导依据是极大似然法估计,而非最小二乘法。
7.1 泊松回归
泊松回归 是用来为计数资料和列联表建模的一种回归分析。泊松回归假设因变量是泊松分布,并假设它平均值的对数可被未知参数的线性组合建模。
泊松回归适合预测计数型结果变量。
需要下载robust包,并加载,用到里面的breslow数据集,这个数据集是对遭受轻微或严重性癫痫病病人的年龄和癫痫病发病数搜集的数据,包含了病人被随机分配到药物组或安慰剂组前八周和后八周两种情况,响应变量是后八周内癫痫病发病数sumY,预测变量为治疗条件Trt,年龄Age和前八周内的基础癫痫病发病数Base,之所以包含基础发病数和年龄,是因为它们对响应变量有潜在的影响,在解释这些协变量后,我们探究的问题是药物治疗是否能够减少癫痫病的发病数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 > data( breslow.dat, package= "robust" ) > breslow.dat ID Y1 Y2 Y3 Y4 Base Age Trt Ysum sumY Age10 Base4 1 104 5 3 3 3 11 31 placebo 14 14 3.1 2.75 2 106 3 5 3 3 11 30 placebo 14 14 3.0 2.75 3 107 2 4 0 5 6 25 placebo 11 11 2.5 1.50 ... 57 228 2 3 0 1 25 21 progabide 6 6 2.1 6.25 58 232 0 0 0 0 13 36 progabide 0 0 3.6 3.25 59 236 1 4 3 2 12 37 progabide 10 10 3.7 3.00 > summary( breslow.dat) ID Y1 Y2 Y3 Y4 Base Age Min. : 101 Min. : 0.00 Min. : 0.00 Min. : 0.00 Min. : 0.00 Min. : 6.0 Min. : 18.0 1 st Qu.: 120 1 st Qu.: 2.00 1 st Qu.: 3.00 1 st Qu.: 2.00 1 st Qu.: 3.00 1 st Qu.: 12.0 1 st Qu.: 23.0 Median : 147 Median : 4.00 Median : 5.00 Median : 4.00 Median : 4.00 Median : 22.0 Median : 28.0 Mean : 168 Mean : 8.95 Mean : 8.36 Mean : 8.44 Mean : 7.31 Mean : 31.2 Mean : 28.3 3 rd Qu.: 216 3 rd Qu.: 10.50 3 rd Qu.: 11.50 3 rd Qu.: 8.00 3 rd Qu.: 8.00 3 rd Qu.: 41.0 3 rd Qu.: 32.0 Max. : 238 Max. : 102.00 Max. : 65.00 Max. : 76.00 Max. : 63.00 Max. : 151.0 Max. : 42.0 Trt Ysum sumY Age10 Base4 placebo : 28 Min. : 0.0 Min. : 0.0 Min. : 1.80 Min. : 1.50 progabide: 31 1 st Qu.: 11.5 1 st Qu.: 11.5 1 st Qu.: 2.30 1 st Qu.: 3.00 Median : 16.0 Median : 16.0 Median : 2.80 Median : 5.50 Mean : 33.0 Mean : 33.0 Mean : 2.83 Mean : 7.81 3 rd Qu.: 36.0 3 rd Qu.: 36.0 3 rd Qu.: 3.20 3 rd Qu.: 10.25 Max. : 302.0 Max. : 302.0 Max. : 4.20 Max. : 37.75 > attach( breslow.dat) > fit <- glm( sumY ~ Base + Trt + Age, data= breslow.dat, family = poisson( link = "log" ) ) > summary( fit) Call: glm( formula = sumY ~ Base + Trt + Age, family = poisson( link = "log" ) , data = breslow.dat) Deviance Residuals: Min 1 Q Median 3 Q Max - 6.057 - 2.043 - 0.940 0.793 11.006 Coefficients: Estimate Std. Error z value Pr( > | z| ) ( Intercept) 1.948826 0.135619 14.37 < 2e-16 * * * Base 0.022652 0.000509 44.48 < 2e-16 * * * Trtprogabide - 0.152701 0.047805 - 3.19 0.0014 * * Age 0.022740 0.004024 5.65 1.6e-08 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 ( Dispersion parameter for poisson family taken to be 1 ) Null deviance: 2122.73 on 58 degrees of freedom Residual deviance: 559.44 on 55 degrees of freedom AIC: 850.7 Number of Fisher Scoring iterations: 5 > coef( fit) ( Intercept) Base Trtprogabide Age 1.94882593 0.02265174 - 0.15270095 0.02274013 > exp ( coef( fit) ) ( Intercept) Base Trtprogabide Age 7.0204403 1.0229102 0.8583864 1.0230007
family = poisson(link = "log")是广义线性模型中泊松回归的写法。
在线性回归中使用的函数,在广义线性模型中都可以使用。例如coef函数可以获取模型的系数,在poisson回归中,因变量以条件均值的对数形式来建模,年龄的回归参数为0.02274013,这表明保持其他预测变量不变,年龄每增加一岁,癫痫病发病数的对数均值将相应地增加0.02274013,截距项表示当预测变量都为0的时候,癫痫病发病数的对数均值。因为年龄都不可能为0,并且调查对象的基础癫痫病发病数均不为0,因此截距无意义。通常在因变量初始尺度上解的回归系数比较困难,因为是对数形式,所以再对其取指数,使用exp函数,可以看到保持其他变量不变,年龄增加一岁期望的癫痫病发病数将乘以1.0230007。说明年龄增加,和较高的癫痫病发病数相关联。一单位治疗条件Trt的变化,平均的癫痫病发病数将乘以0.8583864,也就是说保持基础癫痫病发病数和年龄不变,服药组相对于安慰剂发病率降低了20%,药物是有效的。
7.2 Logistic回归
当通过一系列连续型或类别型预测变量来预测二值型结果变量时,Logistic回归是一个非常有用的工具。
二值型变量在现实为有还是无,是一种二项分布,在现实中很多。
根据危险因素预测某疾病发生的概率。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即“是”或“否”,为两分类变量,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。通过Logistic回归分析,就可以大致了解到底哪些因素是胃癌的危险因素。
这里使用AER包中的Affairs数据集为例:
这个数据集从601个参与者中搜集了9个变量,包括一年来婚外情的频率、参与者的性别、年龄、婚龄、是否有小孩、宗教信仰、教育、职业、对婚姻的自我评分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 > data( "Affairs" , package = "AER" ) > summary( Affairs) affairs gender age yearsmarried children religiousness education Min. : 0.000 female: 315 Min. : 17.50 Min. : 0.125 no : 171 Min. : 1.000 Min. : 9.00 1 st Qu.: 0.000 male : 286 1 st Qu.: 27.00 1 st Qu.: 4.000 yes: 430 1 st Qu.: 2.000 1 st Qu.: 14.00 Median : 0.000 Median : 32.00 Median : 7.000 Median : 3.000 Median : 16.00 Mean : 1.456 Mean : 32.49 Mean : 8.178 Mean : 3.116 Mean : 16.17 3 rd Qu.: 0.000 3 rd Qu.: 37.00 3 rd Qu.: 15.000 3 rd Qu.: 4.000 3 rd Qu.: 18.00 Max. : 12.000 Max. : 57.00 Max. : 15.000 Max. : 5.000 Max. : 20.00 occupation rating Min. : 1.000 Min. : 1.000 1 st Qu.: 3.000 1 st Qu.: 3.000 Median : 5.000 Median : 4.000 Mean : 4.195 Mean : 3.932 3 rd Qu.: 6.000 3 rd Qu.: 5.000 Max. : 7.000 Max. : 5.000 > table( Affairs$ affairs) 0 1 2 3 7 12 451 34 17 19 42 38 > prop.table( table( Affairs$ affairs) ) 0 1 2 3 7 12 0.75041597 0.05657238 0.02828619 0.03161398 0.06988353 0.06322795 > prop.table( table( Affairs$ gender) ) female male 0.5241265 0.4758735 > Affairs$ ynaffair[ Affairs$ affairs > 0 ] <- 1 > Affairs$ ynaffair[ Affairs$ affairs == 0 ] <- 0 > head( Affairs) affairs gender age yearsmarried children religiousness education occupation rating ynaffair 4 0 male 37 10.00 no 3 18 7 4 0 5 0 female 27 4.00 no 4 14 6 4 0 11 0 female 32 15.00 yes 1 12 1 4 0 16 0 male 57 15.00 yes 5 18 6 5 0 23 0 male 22 0.75 no 2 17 6 3 0 29 0 female 32 1.50 no 2 17 5 5 0 > Affairs$ ynaffair <- factor( Affairs$ ynaffair, + levels= c ( 0 , 1 ) , + labels= c ( "No" , "Yes" ) ) > table( Affairs$ ynaffair) No Yes 451 150 > attach( Affairs) > fit <- glm( ynaffair ~ gender + age + yearsmarried + children + + religiousness + education + occupation + rating, + data= Affairs, family= binomial( ) ) > summary( fit) Call: glm( formula = ynaffair ~ gender + age + yearsmarried + children + religiousness + education + occupation + rating, family = binomial( ) , data = Affairs) Deviance Residuals: Min 1 Q Median 3 Q Max - 1.5713 - 0.7499 - 0.5690 - 0.2539 2.5191 Coefficients: Estimate Std. Error z value Pr( > | z| ) ( Intercept) 1.37726 0.88776 1.551 0.120807 gendermale 0.28029 0.23909 1.172 0.241083 age - 0.04426 0.01825 - 2.425 0.015301 * yearsmarried 0.09477 0.03221 2.942 0.003262 * * childrenyes 0.39767 0.29151 1.364 0.172508 religiousness - 0.32472 0.08975 - 3.618 0.000297 * * * education 0.02105 0.05051 0.417 0.676851 occupation 0.03092 0.07178 0.431 0.666630 rating - 0.46845 0.09091 - 5.153 2.56e-07 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 ( Dispersion parameter for binomial family taken to be 1 ) Null deviance: 675.38 on 600 degrees of freedom Residual deviance: 609.51 on 592 degrees of freedom AIC: 627.51 Number of Fisher Scoring iterations: 4 > fit1 <- glm( ynaffair ~ age + yearsmarried + religiousness + + rating, data= Affairs, family= binomial( ) ) > summary( fit1) Call: glm( formula = ynaffair ~ age + yearsmarried + religiousness + rating, family = binomial( ) , data = Affairs) Deviance Residuals: Min 1 Q Median 3 Q Max - 1.6278 - 0.7550 - 0.5701 - 0.2624 2.3998 Coefficients: Estimate Std. Error z value Pr( > | z| ) ( Intercept) 1.93083 0.61032 3.164 0.001558 * * age - 0.03527 0.01736 - 2.032 0.042127 * yearsmarried 0.10062 0.02921 3.445 0.000571 * * * religiousness - 0.32902 0.08945 - 3.678 0.000235 * * * rating - 0.46136 0.08884 - 5.193 2.06e-07 * * * - - - Signif. codes: 0 ‘* * * ’ 0.001 ‘* * ’ 0.01 ‘* ’ 0.05 ‘.’ 0.1 ‘ ’ 1 ( Dispersion parameter for binomial family taken to be 1 ) Null deviance: 675.38 on 600 degrees of freedom Residual deviance: 615.36 on 596 degrees of freedom AIC: 625.36 Number of Fisher Scoring iterations: 4
从回归系数的p-value可以看到,性别、是否有孩子、学历和职业对方程的贡献都不显著,说明出轨和这些关系不大。可以把这些变量去除,重新拟合一次,如fit1,在新模型中每个回归系数都非常显著,p-value均小于0.05,由于fit和fit1两个模型是嵌套关系,可以使用anova函数对它们进行比较。对于广义线性回归可以使用卡方检验。
1 2 3 4 5 6 7 8 9 > anova( fit, fit1, test= "Chisq" ) Analysis of Deviance Table Model 1 : ynaffair ~ gender + age + yearsmarried + children + religiousness + education + occupation + rating Model 2 : ynaffair ~ age + yearsmarried + religiousness + rating Resid. Df Resid. Dev Df Deviance Pr( > Chi) 1 592 609.51 2 596 615.36 - 4 - 5.8474 0.2108
p-value为0.21,卡方检验不显著。证明两次结果差别不大。说明只有四个预测变量的新模型比前面9个完整预测的模型拟合的程度好,所以性别、是否有孩子、学历和职业变量不会显著提高方程的预测精度。可以把这些变量去除掉。
1 2 3 > coef( fit1) ( Intercept) age yearsmarried religiousness rating 1.93083017 - 0.03527112 0.10062274 - 0.32902386 - 0.46136144
回归系数可以看出,在Logistic回归中,响应变量是y为e的对数优势比,回归系数的含义是当其他预测变量不变时,一单位预测变量的变化,可能引起的响应变化对数优势比的变化,由于使用了对数优势比,再对其使用指数运算,回到正常模式:
1 2 3 > exp ( coef( fit1) ) ( Intercept) age yearsmarried religiousness rating 6.8952321 0.9653437 1.1058594 0.7196258 0.6304248
可以看到,婚龄增加一年,婚外情的优势比将乘以1.1058594,相反年龄增加一岁,婚外情的优势比将乘以0.9653437,因此随着婚龄的增加,年龄和宗教信仰与婚姻评分的降低,婚外情优势比将上升。因为预测变量不能等于0,截距项在这里没有意义。
对新数据进行验证,首先创建包含感兴趣变量值的虚拟数据集,为了方便都取数据的平均值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > testdata <- data.frame( rating = c ( 1 , 2 , 3 , 4 , 5 ) , + age = mean( Affairs$ age) , + yearsmarried = mean( Affairs$ yearsmarried) , + religiousness = mean( Affairs$ religiousness) ) > testdata rating age yearsmarried religiousness 1 1 32.48752 8.177696 3.116473 2 2 32.48752 8.177696 3.116473 3 3 32.48752 8.177696 3.116473 4 4 32.48752 8.177696 3.116473 5 5 32.48752 8.177696 3.116473 > testdata$ prob <- predict( fit1, newdata= testdata, type= "response" ) > testdata rating age yearsmarried religiousness prob 1 1 32.48752 8.177696 3.116473 0.5302296 2 2 32.48752 8.177696 3.116473 0.4157377 3 3 32.48752 8.177696 3.116473 0.3096712 4 4 32.48752 8.177696 3.116473 0.2204547 5 5 32.48752 8.177696 3.116473 0.1513079
从上面的结果可以看出,对婚姻的评分越高,婚外情的概率越低。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > testdata <- data.frame( rating = mean( Affairs$ rating) , + age = seq( 17 , 57 , 10 ) , + yearsmarried = mean( Affairs$ yearsmarried) , + religiousness = mean( Affairs$ religiousness) ) > testdata rating age yearsmarried religiousness 1 3.93178 17 8.177696 3.116473 2 3.93178 27 8.177696 3.116473 3 3.93178 37 8.177696 3.116473 4 3.93178 47 8.177696 3.116473 5 3.93178 57 8.177696 3.116473 > testdata$ prob <- predict( fit1, newdata= testdata, type= "response" ) > testdata rating age yearsmarried religiousness prob 1 3.93178 17 8.177696 3.116473 0.3350834 2 3.93178 27 8.177696 3.116473 0.2615373 3 3.93178 37 8.177696 3.116473 0.1992953 4 3.93178 47 8.177696 3.116473 0.1488796 5 3.93178 57 8.177696 3.116473 0.1094738
从上面的结果可以看出,随着年龄的增长,婚外情的概率越低。
7.3 主成分分析
主成分分析和因子分析是统计学中非常重要的分析方法。
主成分分析,Principal Component Analysis,也简称为PCA,是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关的变量称为主成分。主成分其实是对原始变量重新进行线性组合将原先众多具有一定相关性的指标,重新组合为一组的新的相互独立的综合指标。
主成分分析和因子分析模型图:
主成分分析公式:P C 1 = a 1 X 1 = a 2 X 2 + a 3 X 3 + ⋯ + a k X k PC_1=a_1X_1=a_2X_2+a_3X_3+\dots+a_kX_k P C 1 = a 1 X 1 = a 2 X 2 + a 3 X 3 + ⋯ + a k X k
R内置的princomp函数可以进行主成分分析,也可以使用psych包中的函数进行分析,比R提供的内置函数更丰富。
主成分分析与因子分析步骤 :
1、数据预处理;
这里使用psych包中的USJudgeRatings数据集进行演示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > library( psych) 载入程辑包:‘psych’ The following object is masked from ‘package: car’: logit > head( USJudgeRatings) CONT INTG DMNR DILG CFMG DECI PREP FAMI ORAL WRIT PHYS RTEN AARONSON, L.H. 5.7 7.9 7.7 7.3 7.1 7.4 7.1 7.1 7.1 7.0 8.3 7.8 ALEXANDER, J.M. 6.8 8.9 8.8 8.5 7.8 8.1 8.0 8.0 7.8 7.9 8.5 8.7 ARMENTANO, A.J. 7.2 8.1 7.8 7.8 7.5 7.6 7.5 7.5 7.3 7.4 7.9 7.8 BERDON, R.I. 6.8 8.8 8.5 8.8 8.3 8.5 8.7 8.7 8.4 8.5 8.8 8.7 BRACKEN, J.J. 7.3 6.4 4.3 6.5 6.0 6.2 5.7 5.7 5.1 5.3 5.5 4.8 BURNS, E.B. 6.2 8.8 8.7 8.5 7.9 8.0 8.1 8.0 8.0 8.0 8.6 8.6 > fa.parallel( USJudgeRatings, fa= "pc" , n.iter = 100 ) Parallel analysis suggests that the number of factors = NA and the number of components = 1 Warning message: In fa.stats( r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, : The estimated weights for the factor scores are probably incorrect. Try a different factor score estimation method.
生成如上所示的碎石图。碎石图的判定规则为实线与x符号,特征值大于1准则和100次模拟的平行分析。图中虚线表示保存一个主成分,在y=1的水平线上有一个碎石和一条虚线,因此只要保留一个主成分即可。具体碎石图的原理,可以研究平衡分析法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 > pc <- principal( USJudgeRatings, nfactors = 1 , rotate = "none" , scores = FALSE ) > pcPrincipal Components Analysis Call: principal( r = USJudgeRatings, nfactors = 1 , rotate = "none" , scores = FALSE ) Standardized loadings ( pattern matrix) based upon correlation matrix PC1 h2 u2 com CONT - 0.01 9.6e-05 0.9999 1 INTG 0.92 8.4e-01 0.1563 1 DMNR 0.91 8.3e-01 0.1660 1 DILG 0.97 9.4e-01 0.0613 1 CFMG 0.96 9.3e-01 0.0723 1 DECI 0.96 9.2e-01 0.0764 1 PREP 0.98 9.7e-01 0.0299 1 FAMI 0.98 9.5e-01 0.0469 1 ORAL 1.00 9.9e-01 0.0091 1 WRIT 0.99 9.8e-01 0.0195 1 PHYS 0.89 8.0e-01 0.2014 1 RTEN 0.99 9.7e-01 0.0275 1 PC1 SS loadings 10.13 Proportion Var 0.84 Mean item complexity = 1 Test of the hypothesis that 1 component is sufficient. The root mean square of the residuals ( RMSR) is 0.05 with the empirical chi square 12.56 with prob < 1 Fit based upon off diagonal values = 1
PC1列包含了成分载荷,指观测变量与主成分的相关系数,如果提取不止一个主成分,比如将nfactors参数设置为2或3,还会有PC2,PC3等成分。
h2列指成分公因子的方差,它是主成分对每个变量的方差解释度。u2列指的是主成分唯一性,它是方差无法被主成分解释的比例,例如体能PHYS有89%的方差能够被第一主成分来解释。
SS loadings表示与主成分相关联的特征值。指的是特定主成分相关联的标准化后的方差值。
Proportion Var表示每个主成分对整个数据集的解释程度,可以看到第一主成分解释了12个变量84%的方差。
将scores参数设置为TRUE,就可以获得每个变量的得分,如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 > pc <- principal( USJudgeRatings, nfactors = 1 , rotate = "none" , scores = TRUE ) > pcPrincipal Components Analysis Call: principal( r = USJudgeRatings, nfactors = 1 , rotate = "none" , scores = TRUE ) Standardized loadings ( pattern matrix) based upon correlation matrix PC1 h2 u2 com CONT - 0.01 9.6e-05 0.9999 1 INTG 0.92 8.4e-01 0.1563 1 DMNR 0.91 8.3e-01 0.1660 1 DILG 0.97 9.4e-01 0.0613 1 CFMG 0.96 9.3e-01 0.0723 1 DECI 0.96 9.2e-01 0.0764 1 PREP 0.98 9.7e-01 0.0299 1 FAMI 0.98 9.5e-01 0.0469 1 ORAL 1.00 9.9e-01 0.0091 1 WRIT 0.99 9.8e-01 0.0195 1 PHYS 0.89 8.0e-01 0.2014 1 RTEN 0.99 9.7e-01 0.0275 1 PC1 SS loadings 10.13 Proportion Var 0.84 Mean item complexity = 1 Test of the hypothesis that 1 component is sufficient. The root mean square of the residuals ( RMSR) is 0.05 with the empirical chi square 12.56 with prob < 1 Fit based upon off diagonal values = 1 > pc$ scores PC1 AARONSON, L.H. - 0.18400648 ALEXANDER, J.M. 0.74765156 ARMENTANO, A.J. 0.07072468 BERDON, R.I. 1.13651889 BRACKEN, J.J. - 2.15848207 BURNS, E.B. 0.76821742 CALLAHAN, R.J. 1.22243063 COHEN, S.S. - 2.51260343 DALY, J.J. 1.14963289 DANNEHY, J.F. 0.32918115 DEAN, H.H. - 0.10589377 DEVITA, H.J. - 0.45257054 DRISCOLL, P.J. - 0.21014722 GRILLO, A.E. - 1.01338259 HADDEN, W.L.JR. 0.42501399 HAMILL, E.C. - 0.13973759 HEALEY.A.H. - 0.91030943 HULL, T.C. - 0.22553233 LEVINE, I. 0.20145341 LEVISTER, R.L. - 1.36839157 MARTIN, L.F. - 0.57128247 MCGRATH, J.F. - 0.97984173 MIGNONE, A.F. - 1.99621925 MISSAL, H.M. - 0.02581675 MULVEY, H.M. 1.05284946 NARUK, H.J. 1.42897516 O'BRIEN,F.J. 0.47123628 O' SULLIVAN, T.J. 1.09004545 PASKEY, L. 0.59472217 RUBINOW, J.E. 1.50120742 SADEN.G.A. 0.34527687 SATANIELLO, A.G. 0.17036943 SHEA, D.M. 0.81143377 SHEA, J.F.JR. 1.12983152 SIDOR, W.J. - 2.15582532 SPEZIALE, J.A. 0.63632965 SPONZO, M.J. 0.37901740 STAPLETON, J.F. 0.22614913 TESTO, R.J. - 0.66166162 TIERNEY, W.L.JR. 0.42466794 WALL, R.A. - 0.81315467 WRIGHT, D.B. 0.45956919 ZARRILLI, K.J. - 0.28764663
再看第二个案例:Harman23.cor数据集
Harman23.cor数据集包含了305个女孩8个身体测量指标。在这个例子中,数据集由变量的相关系数组成,而不是原始数据集,用主成分分析,使用较少的变量替换原始身体指标。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Harman23.cor$ cov height arm.span forearm lower.leg weight bitro.diameter chest.girth chest.width height 1.000 0.846 0.805 0.859 0.473 0.398 0.301 0.382 arm.span 0.846 1.000 0.881 0.826 0.376 0.326 0.277 0.415 forearm 0.805 0.881 1.000 0.801 0.380 0.319 0.237 0.345 lower.leg 0.859 0.826 0.801 1.000 0.436 0.329 0.327 0.365 weight 0.473 0.376 0.380 0.436 1.000 0.762 0.730 0.629 bitro.diameter 0.398 0.326 0.319 0.329 0.762 1.000 0.583 0.577 chest.girth 0.301 0.277 0.237 0.327 0.730 0.583 1.000 0.539 chest.width 0.382 0.415 0.345 0.365 0.629 0.577 0.539 1.000 $ center[ 1 ] 0 0 0 0 0 0 0 0 $ n.obs[ 1 ] 305 > fa.parallel( Harman23.cor$ cov, n.obs = 302 , fa= "pc" , n.iter = 100 , show.legend = FALSE ) Parallel analysis suggests that the number of factors = NA and the number of components = 2
图中有两个碎石在y=1之上,所以需要两个主成分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 > pc <- principal( Harman23.cor$ cov, nfactors = 2 , rotate = "none" ) > pcPrincipal Components Analysis Call: principal( r = Harman23.cor$ cov, nfactors = 2 , rotate = "none" ) Standardized loadings ( pattern matrix) based upon correlation matrix PC1 PC2 h2 u2 com height 0.86 - 0.37 0.88 0.123 1.4 arm.span 0.84 - 0.44 0.90 0.097 1.5 forearm 0.81 - 0.46 0.87 0.128 1.6 lower.leg 0.84 - 0.40 0.86 0.139 1.4 weight 0.76 0.52 0.85 0.150 1.8 bitro.diameter 0.67 0.53 0.74 0.261 1.9 chest.girth 0.62 0.58 0.72 0.283 2.0 chest.width 0.67 0.42 0.62 0.375 1.7 PC1 PC2 SS loadings 4.67 1.77 Proportion Var 0.58 0.22 Cumulative Var 0.58 0.81 Proportion Explained 0.73 0.27 Cumulative Proportion 0.73 1.00 Mean item complexity = 1.7 Test of the hypothesis that 2 components are sufficient. The root mean square of the residuals ( RMSR) is 0.05 Fit based upon off diagonal values = 0.99
结果显示第一主成分解释了身体测量指标58%的方差,第二主成分解释了身体测量指标22%的方差,两者总共解释了81%的方差(Cumulative Var),对于高度h变量,两者共解释了88%的方差。
旋转是一系列将成分载荷变得更容易解释的数学方法,它们尽可能地对成分去噪,旋转方法有两种,使旋转的成分保持不相关的正交旋转和让它们变得相关的斜交旋转。旋转方法也会依据去噪定义的不同而不同。最流行的正交旋转是方差极大旋转。它试图对载荷矩阵的列进行去噪,使得每个成分只是由一组有限的变量来解释。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 > pc <- principal( Harman23.cor$ cov, nfactors = 2 , rotate = "varimax" ) > pcPrincipal Components Analysis Call: principal( r = Harman23.cor$ cov, nfactors = 2 , rotate = "varimax" ) Standardized loadings ( pattern matrix) based upon correlation matrix RC1 RC2 h2 u2 com height 0.90 0.25 0.88 0.123 1.2 arm.span 0.93 0.19 0.90 0.097 1.1 forearm 0.92 0.16 0.87 0.128 1.1 lower.leg 0.90 0.22 0.86 0.139 1.1 weight 0.26 0.88 0.85 0.150 1.2 bitro.diameter 0.19 0.84 0.74 0.261 1.1 chest.girth 0.11 0.84 0.72 0.283 1.0 chest.width 0.26 0.75 0.62 0.375 1.2 RC1 RC2 SS loadings 3.52 2.92 Proportion Var 0.44 0.37 Cumulative Var 0.44 0.81 Proportion Explained 0.55 0.45 Cumulative Proportion 0.55 1.00 Mean item complexity = 1.1 Test of the hypothesis that 2 components are sufficient. The root mean square of the residuals ( RMSR) is 0.05 Fit based upon off diagonal values = 0.99
列的名字由PC变为RC,表示列的名字被旋转了,观察RC1列的载荷,可以看出第一主成分由前四个变量来解释,主要都是与高度相关的变量,RC2列的载荷表示第二主成分主要由变量5到变量8这四个变量来解释,主要都是与重量相关的变量。两个主成分仍不相关,对变量的解释性不变。这是因为变量的群组没有发生变化,另外两个主成分旋转后的累计方差解释性没有变化,还是81%。变的只是各个主成分对方差的解释度。成分1从58%变为44%,成分2从22%变为37%,各成分的方差解释度趋同,只能称它们为成分,而不是主成分。
7.4 因子分析
探索性因子分析法Exploratory Factor Analysis,简称为EFA,是一系列用来发现一组变量的潜在结构的方法。它通过寻找一组更小的、潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系。
因子分析公式:X i = a 1 F 1 + a 2 F 2 + ⋯ + a p F p + U i X_i=a_1F_1+a_2F_2+\dots+a_pF_p+U_i X i = a 1 F 1 + a 2 F 2 + ⋯ + a p F p + U i
主成分分析公式:P C 1 = a 1 X 1 = a 2 X 2 + a 3 X 3 + ⋯ + a k X k PC_1=a_1X_1=a_2X_2+a_3X_3+\dots+a_kX_k P C 1 = a 1 X 1 = a 2 X 2 + a 3 X 3 + ⋯ + a k X k
比如:语文、数学、外语、物理、化学、生物、历史、地理、政治
主成分分析 :语文、数学、外语、文科或者理科
因子分析 :逻辑推理(数学、物理、化学,生物),语言天赋(语文、外语),逻辑分析(历史、政治、地理)。
主成分与因子分析比较
相同点:
都对原始数据进行降维处理;
都消除了原始指标的相关性对综合评价所造成的信息重复的影响;
构造综合评价时所涉及的权数具有客观性;
在信息损失不大的前提下,减少了评价工作量。
不同点:
用较少的变量表示原来的样本;
目的是样本数据信息损失最小的原则下,对高维变量进行降维。
参数估计,一般是求相关矩阵的特征值和相应的特征向量,取前几个计算主成分。
应用:应用较少变量来解释各个样本的特征。
因子分析:
用较少的因子表示原来的变量;
目的是尽可能保持原变量相互关系,寻找变量的公共因子;
参数估计,指定几个公因子,将其还原成相关系数矩阵,在和原样本相关矩阵最相似原则下,估计各个公因子的估计值;
应用:找到具有本质意义的少量因子来归纳原来变量的特征。
因子分析的评价结果没有主成分分析准确,计算工作量也比主成分分析工作量大,但是公共因子比主成分更容易被解释。
主成分分析与因子分析步骤 :
1、数据预处理;
也是通过碎石图判断选择因子的数目。
R内置的factanal函数可以进行因子分析,这里使用psych包中的ability.cov数据集进行示例演示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > library( psych) > ability.cov$ cov general picture blocks maze reading vocab general 24.641 5.991 33.520 6.023 20.755 29.701 picture 5.991 6.700 18.137 1.782 4.936 7.204 blocks 33.520 18.137 149.831 19.424 31.430 50.753 maze 6.023 1.782 19.424 12.711 4.757 9.075 reading 20.755 4.936 31.430 4.757 52.604 66.762 vocab 29.701 7.204 50.753 9.075 66.762 135.292 $ center[ 1 ] 0 0 0 0 0 0 $ n.obs[ 1 ] 112
ability.cov数据集:
112个人参与了六个测验,包括非语言的普通智力测验(general)、画图测验(picture)、积木图案测验(blocks)、迷津测验(maze)、阅读测验(reading)和词汇测验(vocab)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 > options( digits = 2 ) > covariances <- ability.cov$ cov> correlations <- cov2cor( covariances) > correlations general picture blocks maze reading vocab general 1.00 0.47 0.55 0.34 0.58 0.51 picture 0.47 1.00 0.57 0.19 0.26 0.24 blocks 0.55 0.57 1.00 0.45 0.35 0.36 maze 0.34 0.19 0.45 1.00 0.18 0.22 reading 0.58 0.26 0.35 0.18 1.00 0.79 vocab 0.51 0.24 0.36 0.22 0.79 1.00 > fa.parallel( correlations, fa= "both" , n.obs = 112 , n.iter = 100 ) Parallel analysis suggests that the number of factors = 2 and the number of components = 1 There were 24 warnings ( use warnings( ) to see them)
fa.parallel函数判断提取的因子数,将fa参数设置为both,表示既做主成分又做因子成分的碎石图,这是为了比较二者的区别,也可以单独设置为pc或fa。
观察图中EFA的结果,显示需要提取两个因子,因子是图中三角形部分,碎石检验的前两个特征值都在拐角之上,并且大于基于100次模拟数据矩阵的特征值的均值,对于EFA,图中建议选取两个因子。接下来可以使用FA函数进行因子分析。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 > fa <- fa( correlations, nfactors = 2 , rotate = "none" , fm= "pa" ) > faFactor Analysis using method = pa Call: fa( r = correlations, nfactors = 2 , rotate = "none" , fm = "pa" ) Standardized loadings ( pattern matrix) based upon correlation matrix PA1 PA2 h2 u2 com general 0.75 0.07 0.57 0.432 1.0 picture 0.52 0.32 0.38 0.623 1.7 blocks 0.75 0.52 0.83 0.166 1.8 maze 0.39 0.22 0.20 0.798 1.6 reading 0.81 - 0.51 0.91 0.089 1.7 vocab 0.73 - 0.39 0.69 0.313 1.5 PA1 PA2 SS loadings 2.75 0.83 Proportion Var 0.46 0.14 Cumulative Var 0.46 0.60 Proportion Explained 0.77 0.23 Cumulative Proportion 0.77 1.00 Mean item complexity = 1.5 Test of the hypothesis that 2 factors are sufficient. The degrees of freedom for the null model are 15 and the objective function was 2.5 The degrees of freedom for the model are 4 and the objective function was 0.07 The root mean square of the residuals ( RMSR) is 0.03 The df corrected root mean square of the residuals is 0.06 Fit based upon off diagonal values = 0.99 Measures of factor score adequacy PA1 PA2 Correlation of ( regression) scores with factors 0.96 0.92 Multiple R square of scores with factors 0.93 0.84 Minimum correlation of possible factor scores 0.86 0.68
fa函数用法如下:
1 2 3 4 5 fa( r, nfactors= 1 , n.obs = NA , n.iter= 1 , rotate= "oblimin" , scores= "regression" , residuals= FALSE , SMC= TRUE , covar= FALSE , missing = FALSE , impute= "median" , min.err = 0.001 , max.iter = 50 , symmetric= TRUE , warnings= TRUE , fm= "minres" , alpha= .1 , p= .05 , oblique.scores= FALSE , np.obs= NULL , use= "pairwise" , cor= "cor" , correct= .5 , weight= NULL , n.rotations= 1 , hyper= .15 , ...)
r是相关系数矩阵或原始数据矩阵,这里使用的是相关系数矩阵;nfactors设定提取的因子数;n.obs是观测数,也就是样本数;rotate设定旋转的方法;scores是是否计算因子得分,默认不计算;这些与主成分分析函数都是一致的,与PCA不同的是,提取公共因子的方法有很多,包括最大似然法、主轴迭代法、加权最小二乘法、广义加权最小二乘法和最小残差法,通过fm选项进行设置,默认使用的是极小残差法。这里选择使用主轴迭代法,将fm设置为pa。
这里不需要summary函数了,因为summary信息很少,都是统计信息。
1 2 3 4 5 6 7 8 9 > summary( fa) Factor analysis with Call: fa( r = correlations, nfactors = 2 , rotate = "none" , fm = "pa" ) Test of the hypothesis that 2 factors are sufficient. The degrees of freedom for the model is 4 and the objective function was 0.07 The root mean square of the residuals ( RMSA) is 0.03 The df corrected root mean square of the residuals is 0.06
下面介绍一下因子的旋转,和主成分旋转类似,也是希望成分载荷矩阵变为更容易解释的数学方法,可以使用正交旋转和斜交旋转两种方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 > fa.varimax <- fa( correlations, nfactors = 2 , rotate = "varimax" , fm= "pa" ) > fa.varimaxFactor Analysis using method = pa Call: fa( r = correlations, nfactors = 2 , rotate = "varimax" , fm = "pa" ) Standardized loadings ( pattern matrix) based upon correlation matrix PA1 PA2 h2 u2 com general 0.49 0.57 0.57 0.432 2.0 picture 0.16 0.59 0.38 0.623 1.1 blocks 0.18 0.89 0.83 0.166 1.1 maze 0.13 0.43 0.20 0.798 1.2 reading 0.93 0.20 0.91 0.089 1.1 vocab 0.80 0.23 0.69 0.313 1.2 PA1 PA2 SS loadings 1.83 1.75 Proportion Var 0.30 0.29 Cumulative Var 0.30 0.60 Proportion Explained 0.51 0.49 Cumulative Proportion 0.51 1.00 Mean item complexity = 1.3 Test of the hypothesis that 2 factors are sufficient. The degrees of freedom for the null model are 15 and the objective function was 2.5 The degrees of freedom for the model are 4 and the objective function was 0.07 The root mean square of the residuals ( RMSR) is 0.03 The df corrected root mean square of the residuals is 0.06 Fit based upon off diagonal values = 0.99 Measures of factor score adequacy PA1 PA2 Correlation of ( regression) scores with factors 0.96 0.92 Multiple R square of scores with factors 0.91 0.85 Minimum correlation of possible factor scores 0.82 0.71
reading和vocab在第一因子上载荷较大,画图、积木和迷宫在第二因子上载荷较大,非语言的普通智力测试在两个因子上载荷较为平均,这表明存在一个语言智力因子和一个非语言的智力因子,使用正交旋转将人为地强制两个因子不相关,如果想允许两个因子相关,可以使用斜交旋转法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 > fa.promax <- fa( correlations, nfactors = 2 , rotate = "promax" , fm= "pa" ) > fa.promaxFactor Analysis using method = pa Call: fa( r = correlations, nfactors = 2 , rotate = "promax" , fm = "pa" ) Standardized loadings ( pattern matrix) based upon correlation matrix PA1 PA2 h2 u2 com general 0.37 0.48 0.57 0.432 1.9 picture - 0.03 0.63 0.38 0.623 1.0 blocks - 0.10 0.97 0.83 0.166 1.0 maze 0.00 0.45 0.20 0.798 1.0 reading 1.00 - 0.09 0.91 0.089 1.0 vocab 0.84 - 0.01 0.69 0.313 1.0 PA1 PA2 SS loadings 1.83 1.75 Proportion Var 0.30 0.29 Cumulative Var 0.30 0.60 Proportion Explained 0.51 0.49 Cumulative Proportion 0.51 1.00 With factor correlations of PA1 PA2 PA1 1.00 0.55 PA2 0.55 1.00 Mean item complexity = 1.2 Test of the hypothesis that 2 factors are sufficient. The degrees of freedom for the null model are 15 and the objective function was 2.5 The degrees of freedom for the model are 4 and the objective function was 0.07 The root mean square of the residuals ( RMSR) is 0.03 The df corrected root mean square of the residuals is 0.06 Fit based upon off diagonal values = 0.99 Measures of factor score adequacy PA1 PA2 Correlation of ( regression) scores with factors 0.97 0.94 Multiple R square of scores with factors 0.93 0.88 Minimum correlation of possible factor scores 0.86 0.77
上述为斜交旋转的结果,根据以上结果可以看出正交旋转和斜交旋转的不同之处,对于正交旋转,因子分析的重点在于因子结构矩阵,而对于斜交旋转,因子分析会考虑三个矩阵:因子结构矩阵、因子模式矩阵和因子关联矩阵。因子模式矩阵即标准化后的回归系数矩阵,它列出因子预测变量的权重,因子关联矩阵也就是因子相关系数矩阵,使用factor.plot或fa.diagram函数可以绘制正交或斜交结果的图形。
1 > factor.plot( fa.promax, labels = rownames( fa.promax$ loadings) )
1 > fa.diagram( fa.varimax, simple = FALSE )
1 2 3 4 5 6 7 8 9 > fa <- fa( correlations, nfactors = 2 , rotate = "none" , fm= "pa" , score = TRUE ) > fa$ weights PA1 PA2 general 0.162 0.1428 picture 0.061 0.0754 blocks 0.407 0.7099 maze 0.035 0.0086 reading 0.452 - 0.7447 vocab 0.123 - 0.1468
在fa函数中如果添加score=TRUE选项,就可以计算因子得分,另外还可以得到得分系数。得分在返回对象的weights元素中。
7.5 购物篮分析
有个经典的故事:啤酒和尿布
这里使用arules包中的apriori函数进行建模,这个函数相当于lm和aov函数。
这里使用Groceries数据集,Groceries就是购物篮的意思,里面统计顾客购物篮中的商品。Groceries数据集的属性和其他数据集不同,没有办法打印出来。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 > fit <- apriori( Groceries, parameter = list ( support= 0.01 , confidence= 0.5 ) ) Apriori Parameter specification: confidence minval smax arem aval originalSupport maxtime support minlen maxlen target ext 0.5 0.1 1 none FALSE TRUE 5 0.01 1 10 rules TRUE Algorithmic control: filter tree heap memopt load sort verbose 0.1 TRUE TRUE FALSE TRUE 2 TRUE Absolute minimum support count: 98 set item appearances ...[ 0 item( s) ] done [ 0.00 s] . set transactions ...[ 169 item( s) , 9835 transaction( s) ] done [ 0.00 s] . sorting and recoding items ... [ 88 item( s) ] done [ 0.00 s] . creating transaction tree ... done [ 0.00 s] . checking subsets of size 1 2 3 4 done [ 0.00 s] . writing ... [ 15 rule( s) ] done [ 0.00 s] . creating S4 object ... done [ 0.00 s] . > fitset of 15 rules > summary( fit) set of 15 rules rule length distribution ( lhs + rhs) : sizes 3 15 Min. 1 st Qu. Median Mean 3 rd Qu. Max. 3 3 3 3 3 3 summary of quality measures: support confidence coverage lift count Min. : 0.0101 Min. : 0.50 Min. : 0.017 Min. : 1.98 Min. : 99 1 st Qu.: 0.0117 1 st Qu.: 0.52 1 st Qu.: 0.021 1 st Qu.: 2.04 1 st Qu.: 116 Median : 0.0123 Median : 0.52 Median : 0.024 Median : 2.20 Median : 121 Mean : 0.0132 Mean : 0.54 Mean : 0.025 Mean : 2.30 Mean : 129 3 rd Qu.: 0.0140 3 rd Qu.: 0.57 3 rd Qu.: 0.026 3 rd Qu.: 2.43 3 rd Qu.: 138 Max. : 0.0223 Max. : 0.59 Max. : 0.043 Max. : 3.03 Max. : 219 mining info: data ntransactions support confidence Groceries 9835 0.01 0.5 call apriori( data = Groceries, parameter = list ( support = 0.01 , confidence = 0.5 ) ) > inspect( fit) lhs rhs support confidence coverage lift count [ 1 ] { curd, yogurt} = > { whole milk} 0.010 0.58 0.017 2.3 99 [ 2 ] { other vegetables, butter} = > { whole milk} 0.011 0.57 0.020 2.2 113 [ 3 ] { other vegetables, domestic eggs} = > { whole milk} 0.012 0.55 0.022 2.2 121 [ 4 ] { yogurt, whipped/ sour cream} = > { whole milk} 0.011 0.52 0.021 2.1 107 [ 5 ] { other vegetables, whipped/ sour cream} = > { whole milk} 0.015 0.51 0.029 2.0 144 [ 6 ] { pip fruit, other vegetables} = > { whole milk} 0.014 0.52 0.026 2.0 133 [ 7 ] { citrus fruit, root vegetables} = > { other vegetables} 0.010 0.59 0.018 3.0 102 [ 8 ] { tropical fruit, root vegetables} = > { other vegetables} 0.012 0.58 0.021 3.0 121 [ 9 ] { tropical fruit, root vegetables} = > { whole milk} 0.012 0.57 0.021 2.2 118 [ 10 ] { tropical fruit, yogurt} = > { whole milk} 0.015 0.52 0.029 2.0 149 [ 11 ] { root vegetables, yogurt} = > { other vegetables} 0.013 0.50 0.026 2.6 127 [ 12 ] { root vegetables, yogurt} = > { whole milk} 0.015 0.56 0.026 2.2 143 [ 13 ] { root vegetables, rolls/ buns} = > { other vegetables} 0.012 0.50 0.024 2.6 120 [ 14 ] { root vegetables, rolls/ buns} = > { whole milk} 0.013 0.52 0.024 2.0 125 [ 15 ] { other vegetables, yogurt} = > { whole milk} 0.022 0.51 0.043 2.0 219
如果购物篮里有curd和yogurt,就一定有milk,这个支持度达到了1%,置信度达到了58%。
confidence为置信度,lift类似于相关系数,当lift=1时,表明两个关系并不大,值越大表明相关关系越大,通过这个结果,建议将这些乳制品放一起。
附录 R内置数据集
向量
euro #欧元率,长度为11,每个元素都有命名
landmasses #48个陆地的面积,每个都有命名
precip #长度为70的命名向量
rivers #北美141条河流长度
state.abb #美国50个州的双字母缩写
state.area #美国50个州的面积
state.name #美国50个州怕的全称
因子
state.division #美国50个州的分类,9个类别
state.region #美国50个州的地理分类
矩阵、数组
euro.cross #11种货币的汇率矩阵
freeny.x #每个季度影响收入四个因素的记录
state.x77 #美国50个州的八个指标
USPersonalExpenditure #5个年份在5个消费方向的数据
VADeaths #1940年弗吉尼亚州死亡率(每千人)
volcano #某火山区的地理信息(10米×10米的网格)
WorldPhones #8个区域在7个年份的电话总数
iris3 #3种鸢尾花形态数据
Titanic #泰坦尼克乘员统计
UCBAdmissions #伯克利分校1973年院系、录取和性别的频数
crimtab #3000个男性罪犯左手中指长度和身高关系
HairEyeColor #592人头发颜色、眼睛颜色和性别的频数
occupationalStatus #英国男性父子职业联系
类矩阵
eurodist #欧洲12个城市的距离矩阵,只有下三角部分
Harman23.cor #305个女孩八个形态指标的相关系数矩阵
Harman74.cor #145个儿童24个心理指标的相关系数矩阵
数据框
airquality #纽约1973年5-9月每日空气质量
anscombe #四组x-y数据,虽有相似的统计量,但实际数据差别较大
attenu #多个观测站对加利福尼亚23次地震的观测数据
attitude #30个部门在七个方面的调查结果,调查结果是同一部门35个职员赞成的百分比
beaver1 #一只海狸每10分钟的体温数据,共114条数据
beaver2 #另一只海狸每10分钟的体温数据,共100条数据
BOD #随水质的提高,生化反应对氧的需求(mg/l)随时间(天)的变化
cars #1920年代汽车速度对刹车距离的影响
chickwts #不同饮食种类对小鸡生长速度的影响
esoph #法国的一个食管癌病例对照研究
faithful #一个间歇泉的爆发时间和持续时间
Formaldehyde #两种方法测定甲醛浓度时分光光度计的读数
Freeny #每季度收入和其他四因素的记录
dating from #配对的病例对照数据,用于条件logistic回归
InsectSprays #使用不同杀虫剂时昆虫数目
iris #3种鸢尾花形态数据
LifeCycleSavings #50个国家的存款率
longley #强共线性的宏观经济数据
morley #光速测量试验数据
mtcars #32辆汽车在11个指标上的数据
OrchardSprays #使用拉丁方设计研究不同喷雾剂对蜜蜂的影响
PlantGrowth #三种处理方式对植物产量的影响
pressure #温度和气压
Puromycin #两种细胞中辅因子浓度对酶促反应的影响
quakes #1000次地震观测数据(震级>4)
randu #在VMS1.5中使用FORTRAN中的RANDU三个一组生成随机数字,共400组。 该随机数字有问题。在VMS2.0以上版本已修复。
rock #48块石头的形态数据 sleep #两药物的催眠效果
stackloss #化工厂将氨转为硝酸的数据 swiss #瑞士生育率和社会经济指标
ToothGrowth #VC剂量和摄入方式对豚鼠牙齿的影响 trees #树木形态指标
USArrests #美国50个州的四个犯罪率指标
USJudgeRatings #43名律师的12个评价指标
warpbreaks #织布机异常数据
women #15名女性的身高和体重
列表
state.center #美国50个州中心的经度和纬度
类数据框
ChickWeight #饮食对鸡生长的影响
CO2 #耐寒植物CO2摄取的差异
DNase #若干次试验中,DNase浓度和光密度的关系
Indometh #某药物的药物动力学数据
Loblolly #火炬松的高度、年龄和种源
Orange #桔子树生长数据
Theoph #茶碱药动学数据
时间序列数据
airmiles #美国1937-1960年客运里程营收(实际售出机位乘以飞行里数)
AirPassengers #Box & Jenkins航空公司1949-1960年每月国际航线乘客数
austres #澳大利亚1971-1994每季度人口数(以千为单位)
BJsales #有关销售的一个时间序列
BJsales.lead #前一指标的先行指标(leading indicator)
co2 #1959-1997年每月大气co2浓度(ppm)
discoveries #1860-1959年每年巨大发现或发明的个数
ldeaths #1974-1979年英国每月支气管炎、肺气肿和哮喘的死亡率
fdeaths #前述死亡率的女性部分
mdeaths #前述死亡率的男性部分
freeny.y #每季度收入
JohnsonJohnson #1960-1980年每季度Johnson & Johnson股票的红利
LakeHuron #1875-1972年某一湖泊水位的记录
lh #黄体生成素水平,10分钟测量一次
lynx #1821-1934年加拿大猞猁数据
nhtemp #1912-1971年每年平均温度
Nile #1871-1970尼罗河流量
nottem #1920-1939每月大气温度
presidents #1945-1974年每季度美国总统支持率
UKDriverDeaths #1969-1984年每月英国司机死亡或严重伤害的数目
sunspot.month #1749-1997每月太阳黑子数
sunspot.year #1700-1988每年太阳黑子数
sunspots #1749-1983每月太阳黑子数
treering #归一化的树木年轮数据
UKgas #1960-1986每月英国天然气消耗
USAccDeaths #1973-1978美国每月意外死亡人数
uspop #1790–1970美国每十年一次的人口总数(百万为单位)
WWWusage #每分钟网络连接数
Seatbelts #多变量时间序列。和UKDriverDeaths时间段相同,反映更多因素。
EuStockMarkets #多变量时间序列。欧洲股市四个主要指标的每个工作日记录。